DFT, FFT, IFFT

הכלים הנפוצים ביותר לביצוע אנליזת וסינטזת פורייה הם FFT ו-IFFT. אלו הם אלגוריתמים מבוססי מחשב אופטימליים (מהירים מאוד) שמבצעים תהליך מתמטי מוכלל שנקרא טרנספורמציית פורייה בדידה (DFT). ה-DFT היא הטרנספורמציה המתמטית עצמה שהמידע עובר כשהוא מומר מממלכה אחת לאחרת (זמן לתדר). באופן בסיסי ה-DFT הוא פשוט גרסא איטית של ה-FFT.
FFT, IFFT ו-DFT נעשו חשובים מאוד לדיסיפלינות רבות כאשר מהנדסים הבינו כיצד לדגום מספיק מהר בכדי ליצר מספיק מידע לשחזור צלילים ותופעות אנלוגיות אחרות באופן דיגיטלי. זכרו, הם לא עובדים רק על צלילים, אלא על כל סיגנל מתמשך (תמונות, גלי רדיו, מידע סיסמוגרפי או שוק המניות). FFT של סיגנל ממלכת הזמן לוקח את הדגימות ונותן לנו קבוצה חדש של מספרים, שמייצגים את התדרים, אמפליטודות ופאזות של גלי הסינוס אשר מרכיבים את הצליל שניתחנו. מידע זה הוא זה שמוצג בסונוגרמות שראינו קודם.

כיצד ה-FFT עובד
ה-FFT עובד בדרך ישירה למדי. הוא לוקח פיסת זמן שנקראת מסגרת (מספר מסוים של דגימות) ומתייחס לפיסה זו כמחזור אחד של צורת גל מחזורית. הסיבה שזה עובד היא שרוב הצלילים הם "סטציונרים מקומית". כלומר, לאורך כל זמן קצר, הצליל באמת נראה כמו פונקציה מחזורית רגולרית. נציג דרך התייחסות מתמטית – לקיחת חלון לאורך חלק של סיגנל כלשהו שאנו רוצים להחשיב כפונקציה מחזורית.

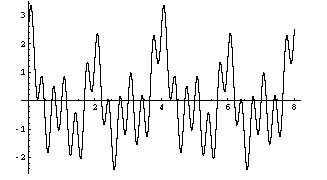
טרנספורמציית פורייה מהירה על קצה המזלג: חישוב רכיבי פורייה
להלן תהליך תלת שלבי לעיבוד צליל דיגיטלי:
1) חלון
2) הרחבה מחזורית
3) טרנספורמציית פורייה (דורש גם דגימה: בקצב ששווה לפעמיים התדר הגבוה ביותר שנדרש). אנו עושים זאת
    בעזרת ה-FFT הידוע לשמצה.

הנה הגרף של פונקציה (מחזורית), (f(t. שימו לב שהפונקציה לא חייבת להיות מחזורית:

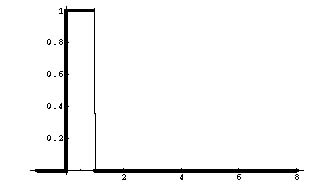
נניח שאנו מעונינים רק בחלק הגרף שבו 0 => t <= 1. אזי הגרף של פונקצית החלון בה עלינו להשתמש יראה כמו הגרף למטה. נקרא לפונקציה (w(t. שימו לב ש-(w(t שווה 1 רק באינטרוול בין 0 ל- 1, ובשאר היא שווה ל- 0:

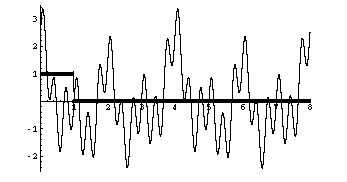
בצעד הראשון של התהליך למציאת רכיבי פורייה עלינו לתחום בחלון את הפונקציה. באיור הבא מתוארת גם פונקצית החלון, (w(t, וגם הפונקציה המקורית (f(t:
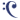
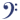