באיור הבא מופיע התיאור הגרפי של (f(t)*w(t. זו הפונקציה המחזורית כפול פונקצית החלון. מאיור זה ברור באיזה חלק של (f(t אנו מעונינים:

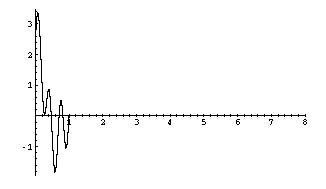
בשלב השני, עלינו להרחיב באופן מחזורי את הפונקציה התחומה, (f(t)*w(t, לאורך ציר הזמן t:

קיבלנו פונקציה מחזורית וע"פ פורייה אנו יכולים כעת לייצגה באמצעות סכום של סינוס וקוסינוס. זהו השלב השלישי. זכרו, אנו יכולים להשתמש גם בחלונות אחרים, לאו דווקא ריבועים. זה נעשה כדי לשפר את ההשפעה של החלונות הרבועים על תוכן התדר של הסיגנל המקורי.

כעת, ברגע שקיבלנו פונקציה מחזורית, כל שעלינו לעשות הוא לגלות, בעזרת ה-FFT, מהם גלי הסינוס המרכיבים את צורת הגל.
כפי שראינו קודם, ניתן לייצג כל צורת גל מחזורית כסכום של גלי סינוס עם הזזת פאזה. בתיאוריה, מספר גלי הסינוס המרכיבים הוא אינסופי – אין גבול למספר רכיבי התדר שצליל יכול להכיל. בפועל, עלינו להגביל את עצמנו למספר ידוע מראש כלשהו. לגבול זה יש השפעה רצינית על רמת הדיוק של האנליזה שלנו.
כך זה עובד: במקום לחפש את תוכן התדר של הצליל בכל התדרים האפשריים (מספר גדול אינסופית – 100.000000001 הרץ, 100.000000002 הרץ, 100.000000003 הרץ וכו') אנו מחלקים את ספקטרום התדרים למספר רצועות תדר שנקראות סלים. גודל הסלים נקבע ע"י מספר הדגימות במסגרת האנליזה שלנו (פיסת הזמן שהוזכרה קודם לכן). מספר הסלים נתון ע"י הנוסחא: מספר הסלים = 2 / גודל המסגרת

גודל המסגרת
נאמר שאנו מחליטים על גודל מסגרת של 1024 דגימות. זו בחירה נפוצה מכיוון שרוב אלגוריתמי FFT שמשמשים לעיבוד צליל דורשים מספר דגימות שהוא ריבוע של מספר אחר (אלו המהירים ביותר) וחשוב לא לקבל מעט או הרבה מדי מהצליל.
גודל מסגרת של 1024 דגימות נותן לנו 512 רצועות תדר. אם נניח שאנו משתמשים בקצב דגימה של 44.1 קילוהרץ, אנו יודעים שיש לנו טווח תדרים של 0-22.05 קילוהרץ. כדי לגלות מהו רוחב כל אחד מסלי התדר, אנו משתמשים בנוסחא: רוחב סל = מספר הסלים / תדר
שבמקרה זה נותן לנו רוחב סל של בערך 43 הרץ. מכיוון שתפיסת התדר היא לוגריתמית, כך ש- 43 הרץ נותנים לנו רזולוציה גרועה בתדרים הנמוכה וטובה יותר בגבוהים. ע"י בחירת גודל מסגרת מסוים ורוחב פס מתאים, אנו נמנעים מבעיה של חישוב מספר אינסופי של רכיבי תדר בצליל. במקום, אנו פשוט מחשבים רכיב אחד לכל רצועת תדר.

יש חבילות תוכנה רבות שיעשו FFT או IFFT למידע שלך, ואח"כ יאפשרו לך לשחק עם תוכן התדר של הצליל. בפרק הבא נדבר על חלק מהדברים המוזרים והנפלאים שניתן לעולל לצליל בממלכת התדר.

לא נתאר כאן את בפרטים כיצד ה-FFT עובד. מה שחשוב הוא שתבינו את הרעיון הכללי של ניתוח צליל ע"י שבירתו לרכיבי התדר שלו, או מהכיוון ההפוך, הרכבת צליל חדש מקבוצת רכיבי תדר. ה-FFT נמצא בשימוש כבר זמן רב ולרוב פלטפורמות המוסיקה הממוחשבות כיום יש כלים לביצוע אנליזת וסינטזת פורייה.