
|
אתם נמצאים כאן: ראשי --> ממלכת התדר --> פורייה וסכום הסינוסים (1) |
|

מה קורה כשאנו מחברים
מספר גלי סינוס יחדיו? נקבל צורת גל מסובכת שהיא סכום של הגלים
הבדידים. תמונה זו היא דוגמא פשוטה, חיברנו רק שני גלי סינוס. ליצירת
צליל מורכב יש צורך במאות ואף אלפי גלי סינוס על מנת שצורת הגל תהייה
מדויקת. אם תביטו על האיור מלמטה למעלה תוכלו לראות שההפך גם נכון –
ניתן לפרק את צורת הגל המורכבת לאוסף של גלי סינוס עצמאיים.
בתמונה: תו של חצוצרה באנליזת FFT – שתי
נקודות מבט.
היתרון של ייצוג צליל
במונחים של סדרת הפורייה שלו הוא שזה מאפשר לנו לעשות מניפולציות על
תוכן התדר באופן ישיר. אם ברצוננו להדגיש את האפקטים של התדר הגבוה
בצליל (להבהיר את הצליל), אנו יכולים פשוט להגדיל את האמפליטודה של
מקדמי פורייה מסדר גבוה. אם ברצוננו להפוך גל מסוג sawtooth לגל מרובע,
אנו יכולים לאפס את מקדמי פורייה של התדרים החלקיים הזוגיים.
|
 |
||
 |
 |

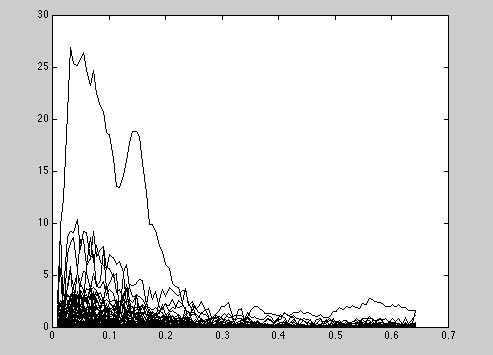

 צליל החצוצרה
צליל החצוצרה