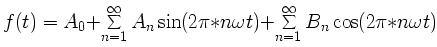פורייה וסכום הסינוסים

בחלק זה ננסה להסביר בפירוט את המשמעות של הרחבת פורייה, בהתבסס על הרעיונות של פאזורים, תדרים חלקיים, ורכיבים סינוסואידים, אותם הצגנו בחלק הקודם.

לפני זמן רב, המדען והמתמטיקאי הצרפתי, ז'אן בפטיסט פורייה (1768-1830) הוכיח את העובדה המתמטית המדהימה ש"כל צורת גל מחזורית ניתנת לביטוי כסכום קבוצה אינסופית של גלי סינוס". התדרים של גלי סינוס אלו חייבים להיות מכפלה של מספר שלם באיזשהו תדר בסיסי. במילים אחרות, אם יש לנו צליל של חצוצרה ב-A אמצעי
(440 הרץ), אנו יודעים ע"פ התיאוריה של פורייה שאנו יכולים לבטא צליל זה כסכום של גלי סינוס: 440 הרץ, 880 הרץ, 1320 הרץ, 1760 הרץ וכך הלאה, או התדר הבסיסי כפול 1, 2, 3, 4… , כל אחד באמפליטודה שונה. עובדה זו מדהימה שכן היא אומרת שעבור כל צורת גל מחזורית (שיש לה גובה גל), אנו למעשה יודעים הכל אודות התדרים החלקיים שלה, פרט לאמפליטודות שלהם.

סדרות פורייה
מהן בדיוק סדרות פורייה ואיך זה מתקשר לפאזורים? אנו משתמשים בפאזורים כדי לייצג את הטונים הבסיסיים שלנו. העובדה המדהימה היא שכל צליל ניתן לייצוג כשילוב של טונים מתדרים שונים עם שינויי אמפליטודה והזזות פאזה. זכרו שקיבלנו רמז לתפיסה זו כשדנו בחיבור פאזורים בחלק הקודם. מכיוון שפאזור הוא למעשה דרך לייצג פונקציה סינוסואידית, המשמעות המתמטית היא שכל צליל ניתן לייצוג כסכום של סינוסואידים. סכום זה נקרא סדרות פורייה. שימו לב שלא הגבלנו צלילים אלו לצלילים מחזוריים – אם כן, היינו צריכים להוסיף את התנאי לגבי כפולות בשלם של התדר הבסיסי. צלילים לא מחזוריים, או א-מחזוריים, מעניינים באותה מידה ואולי אף יותר ממחזוריים, אולם עלינו להשתמש במספר טריקים ממוחשבים כדי לקבל מהם סדרה "הרמונית" למטרות אנליזה וסינתזה.
בואו נרד לפרטים: ראשית נתבונן מה קורה כאשר אנו מחברים שני סינוסואידים בעלי אותו תדר. חיבור של סינוס וקוסינוס נותן הזזת פאזה של סינוס עם אותו התדר:
(A * sin(wt) + B * cos(wt) = C * sin(wt + Z
האמפליטודה של הסכום, C, נתונה ע"י המשוואה:
(C = sqrt(A^2 + B^2
והזזת הפאזה, Z, נתונה ע"י הזווית שהטנגנס שלה שווה ל-A/B. בקיצור:
(Z = arctan(A/B
ניתן לראות זאת בעזרת פאזור. זכרו שהקוסינוס הוא רק הזזת פאזה של סינוס. מכיוון שהם נעים באותו תדר, הם תמיד אינם מסונכרנים ב-pi/2, אז כשאנו מחברים ביניהם אנו מקבלים סינוסואיד נוסף מאותו תדר.

כל פונקציה מחזורית עם מחזור 1 ניתן לכתיבה כ:

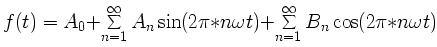
An ו-Bn נקראים מקדמי פורייה של הפונקציה (f(t. למקדם פורייה A0 יש שם מיוחד, הוא נקרא תנאי DC או היסט DC. הוא מייצג את הערך הממוצע של הפונקציה. מקדמי פורייה יוצרים קבוצה של מספרים שנקראים ה"ספקטרום" של הצליל. כשאתם חושבים על המונח ספקטרום אתם בוודאי חושבים על צבעים, כמו הספקטרום של צבעי הקשת. הספקטרום מספר לנו כמה מכל תדר (צבע) יש בצליל.

ערכי An ו-Bn עבור ערכים "קטנים" של n מספקים את מידע ה"תדר הנמוך" והם נקראים מרכיבי פורייה מסדר נמוך. באופן דומה, הערכים הגדולים של n מספקים את מידע ה"תדר הגבוה". רוב הצלילים נוטים להכיל הרבה מידע תדר נמוך – אז למקדמי פורייה מסדר נמוך יש ערך מוחלט גבוה יותר מאשר למקדמי פורייה בעלי תדר גבוה.
המשמעות היא שבאופן תיאורטי ניתן לקחת צליל מורכב, כמו קול של אדם, ולפרק אותו למספר גלי סינוס, כל אחד בתדר, אמפליטודה ופאזה שונים. אלו נקראים המרכיבים הספקטרלים או הסינוסואידים של הצליל. כדי למצוא אותם אנו מבצעים אנליזת פורייה. סינטזת פורייה זהו התהליך ההפוך, שבו אנו לוקחים כמויות שונות של גלי סינוס וסוכמים אותם (מנגנים אותם בו זמנית) כדי ליצור צליל! נשמע מעט פנטסטי, לא? אבל זה עובד. תהליך זה של אנליזה או סינטזה של צליל בהתבסס על מרכיבי גלי הסינוס שלו נקרא טרנספורמציית פורייה על צליל. כשהמחשב עושה זאת הוא משתמש בטכניקה יעילה שנקראת טרנספורמציית פורייה מהירה (או FFT) לאנליזה, והיפוך IFFT) FFT)לסינטזה.