פאזורים

דיברנו כבר על האטומים הבסיסיים של הצליל – גלי הסינוס, או הפונקציה אשר מתארת את הצליל שמופק ע"י ויברציות של מזלג. בפרק זה אנו מדברים הרבה על ממלכת התדר. אם זכור לכם, ליחידות הבסיסיות, גלי הסינוס, היו רק שני פרמטרים: אמפליטודה ותדר. מסתבר שגלי הסינוס המשעממים הללו הולכים לספק לנו את הכלי הבסיסי לאנליזה ולתיאור של הצליל, ובייחוד את מניפולציית התדר הדיגיטלי של הצליל. זוהי הממלכה, מקום בו הרבה גלי סינוס קטנים הם החברים הטובים ביותר שלנו.
אך לפני שאנו מתקדמים יותר מדי, חשוב להבין באופן מלא מהו גל סינוס, וגם נפלא לדעת שאנו יכולים להפוך את העקומות הפשוטות והקטנות הללו למסובכות ביותר. בכל מקרה, כדאי שיהיה ברשותנו מודל נוסף ליצירת פונקציות אלו. מודל זה נקרא פאזור.

תיאור של פאזור
חשוב על גלגל אופניים אשר מושהה במרכזו. אנו הולכים לצבוע את אחד הרדיוסים בגלגל באדום ובסופו נשים חץ אדום. כעת נצייר שני צירים סביב הגלגל – ציר X אופקי וציר Y אנכי. נהיה מעונינים בגובה של ראש החץ ביחס לציר ה-X כאשר הגלגל – הפאזור שלנו – מסתובב נגד כיוון השעון. אם נאתר את מיקום החץ במעגל (מ- 0 ל- 2 פאי) ונמדוד את גובה החץ בציר ה-Y כשהפאזור שלנו מתקדם סביב המעגל, העקומה שנקבל תהיה גל סינוס.

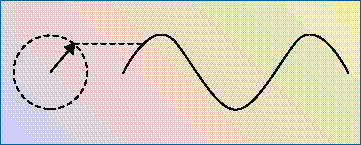
ככל שעובר הזמן הפאזור נע סביב סביב. בכל רגע נתון אנו מודדים את גובה הנקודה מעל ציר ה-X. בואו נעשה דוגמא קטנה: נניח שהגלגל מסתובב בקצב של רוטציה אחת לשניה. זהו התדר שלו, וזה אומר שהמחזור הוא 1 שנייה/רוטציה. זה בדיוק כמו לומר שהגלגל מסתובב בקצב של 360 מעלות לשנייה, או אפילו יותר טוב, 2/2pi רדיאנים לשנייה – אם משתמשים במונחים מתמטיים למדידת זוויות. אם כן, 2 פאי רדיאנים לשנייה הם המהירות הזוויתית של הפאזור.
המשמעות היא שלאחר 0.25 שניות הפאזור עובר pi/2 רדיאנים (90 מעלות), ואחרי 0.5 שניות הוא עובר pi רדיאנים או 180 מעלות, וכן הלאה. אם כן, אנו יכולים לתאר את גודל הזווית שהפאזור עבר בזמן t כפונקציה ששמה (theta(t, וקל לראות ש: theta(t) = 2pi*t
כעת, בואו נתבונן בפונקציה שנתונה ע"י הגובה של החץ לאורך זמן. הדבר הראשון שעלינו לזכור הוא מעט טריגונומטריה. הסינוס והקוסינוס של הזווית נמדדים באמצעות משולש ישר זווית. עבור המשולש ישר הזווית למטה, הסינוס של זווית theta נתון ע"י המשוואה: sin(theta) = a/c

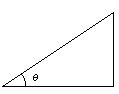
ושימו לב שזה אומר כי: (a = c*sin(theta
נשתמש במשוואה זו הרבה עוד מעט, מכיוון שבתמונה a הוא הגובה של המשולש.
באופן דומה עבור קוסינוס נקבל: (b = c*cos(theta
נחזור חזרה לפאזור שלנו. אנו מעונינים במדידת הגובה בזמן t, שנסמנו (h(t. בזמן t החץ של הפאזור יוצר זווית של (theta(t עם ציר ה-X. לפאזור הבסיסי יש רדיוס 1, ומתקבל היחס הבא:
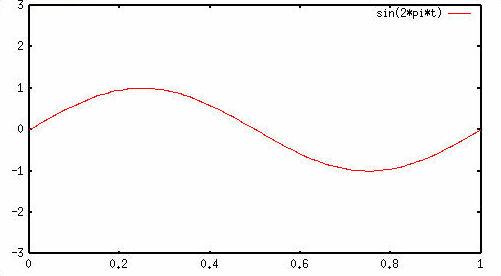
(h(t) = h(t) / radius = sin(theta(t)) = sin(2pi*t
ואנו מקבלים גרף של פונקציה שהוא עקומת הסינוס שלנו. זהו סינוסואיד בסיסי.