כעת, איך אנו יכולים לשנות את העקומה? ובכן, ניתן לשנות את האמפליטודה – זה כמו לשנות את אורך החץ בפאזור. נשאיר את התדר ללא שינוי ונשנה את הרדיוס של הפאזור ל- 3.
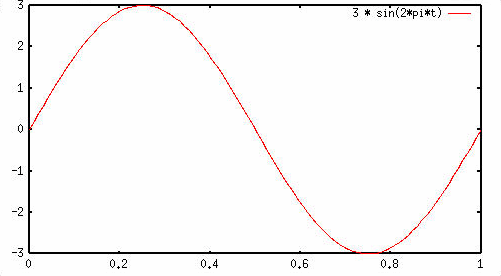
נקבל: sin(2pi*t) = h(t)/3
ומכאן: (h(t) = 3*sin(2pi*t
ונקבל עקומה אחרת שהיא עוד סוג של סינוסואיד (גדול יותר!):

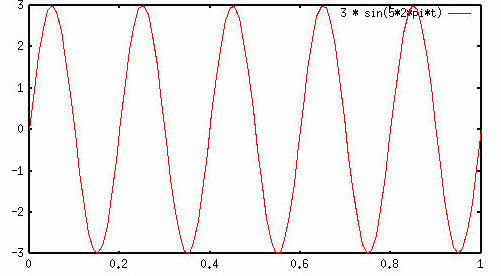
כעת, בואו נשחק עם התדר, שהוא קצב הרוטציה של הפאזור. נעלה אותו מעט ונתחיל לסובב את הפאזור בקצב של 5 רוטציות בשנייה. כלומר, כעת: theta(t) = 5*(2pi*t) = 10pi*t
קל לראות זאת מכיוון שאחרי שנייה נסיים 5 רוטציות שהן סכום כולל של 10/pi רדיאנים. נניח שהרדיוס של הפאזור הוא 3. שוב, בכל רגע נתון נמדוד את הגובה של החץ שמסומן (h(t.
נקבל: sin(theta(t)) = h(t)/3
או: (h(t) = 3*sin(5*2pi*t
ונקבל סינוסואיד מורכב יותר:

באופן כללי, אם הפאזור שלנו היה נע בתדר של w רוטציות לשנייה, והיה לו רדיוס A אז חישוב גובה הפאזור הוא כמו שרטוט הסינוסואיד, ע"פ המשוואה:
(A*sin(w*2pi*t
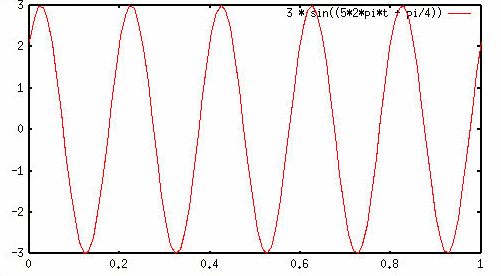
כעת כמעט סיימנו, אך יש דבר אחד נוסף שאנו יכולים לשנות: המקום בו אנו מתחילים את סיבוב הפאזור. לדוגמא, אנו יכולים לקבוע את קצב הסיבוב ל- 5 רוטציות בשנייה עם רדיוס 3, אבל להתחיל את סיבוב הפאזור בזווית של pi/4 רדיאנים. איזו פונקציה תתקבל? ובכן, בזמן t=0 אנו רוצים לבצע את המדידה כשהפאזור בזווית של pi/4, אולם מעבר לכך הכל נשאר כמו קודם. כלומר הפונקציה שאנו מחפשים זהה לזו שמלמעלה, רק עם הזזת פאזה של pi/4. הסינוסואיד המתאים הוא: (h(t) = 3 * sin(5 * 2pi*t + pi/4