הסינוסואיד הכללי ביותר שלנו עם אמפליטודה A, תדר w והזזת פאזה Z הוא מהצורה:
(h(t) = A * sin(w * 2pi*t + Z
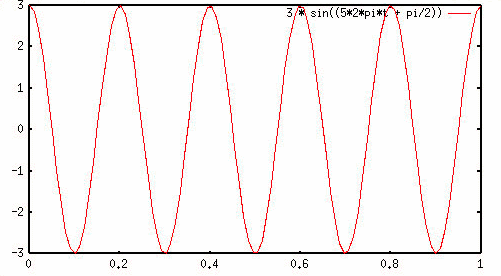
דוגמא מעניינת במיוחד היא מה קורה כאשר אנו בוחרים הזזת פאזה של 90 מעלות או pi/2 רדיאנים. בואו נשאיר את זה פשוט: w שווה לרוטציה אחת בשנייה והאמפליטודה שווה גם היא ל- 1. נקבל את הסינוסואיד הבסיסי שלנו כשהוא מוסט קדימה pi/2. האם זה נראה לכם מוכר? זהו הגרף של פונקציית הקוסינוס!

אתם יכולים לעשות כמה בדיקות משלכם ולראות שזהו גם הגרף שתקבלו אם תעקבו אחר מיקום החץ מציר ה-Y. ובכן, כעת אנו יודעים שקוסינוס הוא הזזת פאזה של סינוס!
(A * cos(w * 2pi*t) = A * sin(w * 2pi*t + Z

התיאוריה של פורייה (Fourier) מספרת לנו שלכל פונקציה מחזורית ניתן להתייחס כסכום (ככל הנראה עם מספר אינסופי של תנאים) של סינוסואידים. זכרו, פונקציה מחזורית היא כל פונקציה שנראית כמו חזרה אינסופית של איזשהו דפוס קבוע. האורך של אותו דפוס בסיסי נקרא המחזור של הפונקציה.
אם T הוא המחזור של הפונקציה המחזורית שלנו, אז אנו יודעים כעת שהתדר שלה הוא 1/T – זה נקרא גם (התדר) הבסיסי של הפונקציה המחזורית, וכעת אנו רואים שכל שאר התדרים שמתרחשים (ושנקראים חלקיים) הם למעשה כפולה בשלם של הבסיסי. התדרים החלקיים נקראים לעיתים אוברטונים (overtones) או הרמוניקות (harmonics). פעמים רבות יש בלבול לגבי האם האוברטון הראשון הוא התדר החלקי השני וכן הלאה. לכן, כדי להיות ספציפיים ולשמור על טרמינולוגיה מודרנית, אנו נתייחס תמיד לתדר החלקי הראשון בתור התדר הזהה לבסיסי.
לדוגמא: נניח שיש לנו גל משולש שחוזר פעם אחת כל 1/100 שניות. אז התדר הבסיסי המתאים הוא 100 הרץ (חוזר 100 פעמים בשנייה). גלים משולשים מכילים רק תדרים חלקיים שהם כפולות אי זוגיות של הבסיסי (לכפולות הזוגיות אין אנרגיה – למעשה, עובדה זו נכונה לכל צורות הגל שיש להן סימטרייה "אי זוגית" בדומה לגל המשולש).

הוספה זו של תדרים חלקיים ליצירת צורת גל מורכבת עשויה להיות הגיונית מבחינה אקוסטית, אך בכדי להבין באמת כיצד להוסיף פאזורים, מנקודת מבט מתמטית, ראשית עלינו להבין כיצד להוסיף וקטורים, או חצים.
איך עלינו להגדיר אריתמטיקה של חצים? זה נשמע מצחיק, אך למעשה זוהי הכללה טבעית למדי של מה שאנו כבר יודעים על סכימת מספרים רגילים. האם אתם זוכרים את מודל "ציר המספרים" לחיבור מספרים? כשמוסיפים מספר שלילי נעים שמאלה על הציר, וכשמוסיפים מספר חיובי נעים ימינה. ניתן לחשוב על מספרים רגילים כעל חצים על ציר המספרים. אז חיבור כל שני מספרים פירושו לקיחת שני החצים המתאימים והנחתם אחד אחרי השני, ראש לזנב. הסכום הוא אז החץ מנקודת המקור ועד לנקודה אליה הגענו מ"חיבור" שני החצים.
מה שלמעשה אנו עושים כאן, הוא לחשוב על מספרים כעל וקטורים. יש להם אורך וכיוון (במקרה זה חיובי או שלילי, או בפרט 0 רדיאנים או pi רדיאנים).
כעת, כדי לחבר פאזורים עלינו להגדיל את ראיית העולם שלנו ולהרשות לחצים לא לפנות רק לשני כיוונים, אלא
ל- 2pi כיוונים. במילים אחרות, נרשה לחצים שלנו לפנות לכל כיוון במישור. כעת נחבר כמו קודם: נניח אותם ראש לזנב ונצייר חץ מהמקור לנקודת היעד הסופית.

לסיכום, כדי לחבר פאזורים אנו מבצעים את הפעולות הבאות: בכל רגע שהפאזורים שלנו מסתובבים אנו מחברים את שני החצים. באופן זה אנו מקבלים חץ חדש שמסתובב (הסכום) בתדר כלשהו – זהו פאזור חדש. כעת קל לראות שסכום של שני פאזורים בעלי אותו תדר מניב פאזור חדש עם אותו תדר. למשל, הסכום של קוסינוס וסינוס עם אותו תדר הוא פשוט הזזת פאזה של סינוס בעל אותו תדר ועם אמפליטודה חדשה שנתונה ע"י השורש הריבועי של סכום הריבועים של שני הפאזורים המקוריים. זהו פשוט משפט פיתגורס.