



| |
_  | |||
דחיסת התמרה דחיסת התמרה שונה מהשיטות שתיארנו עד כה בכך, שהדחיסה שוב אינה מתבצעת על התמונה עצמה, אלא על התמרה שלה. הרעיון בבסיס דחיסת ההתמרה הוא שבהתמרת התמונה, פילוג הערכים עשוי להיות מתאים יותר לדחיסה, מאשר בתמונה עצמה. אחת הסיבות העיקריות למיותרות בתמונה היא המתאם המרחבי הגבוה, שמאפשר לשערך ערך בנקודה על סמך ערכים בסביבתה. לאחר התמרה לתחום התדר המרחבי, המתאם הגבוה מתבטא בכך שרוב רובו של במידע החזותי מרוכז למספר קטן יחסית של מקדמים (כלומר נקודות התמרה), באזור התדרים הנמוכים. דוגמה קיצונית לכך היא תמונה בעלת בהירות אחידה לחלוטין: לאחר התמרה ניתן לתארה באופן מדויק ומלא ע"י נקודת התמרה אחת בלבד (של התדר המרחבי אפס), במקום ע"י N*N נקודות בתמונה עצמה. במרבית התמונות התיאור כמובן מורכב יותר, אולם, כאמור, רוב המידע מרוכז בתדרים הנמוכים, שמקדמיהם גדולים יחסית למקדמי התדרים הגבוהים. נוסף לכך, רגישות העין בתדרים הגבוהים היא נמוכה יחסית. כתוצאה משתי עובדות אלה, ניתן לכמות את מקדמי ההתמרה כתלות בתדר המרחבי שהם מייצגים: ככל שהתדר גבוה יותר, הכימוי יכול להיות גס יותר. בכך טמון רווח גדול מבחינת הדחיסה, משום שאת רוב רובן של נקודות ההתמרה ניתן לכמות באופן גס, או לאפסן לחלוטין (כלומר, להתעלם מהן). יש להדגיש, כי בכל דחיסות ההתמרה, הדחיסה המתקבלת לא מן ההתמרה עצמה (שכמות המידע הגולמי בה זהה לזו שבתמונה), אלא מכימוי ומקידוד מקדמי ההתמרה. 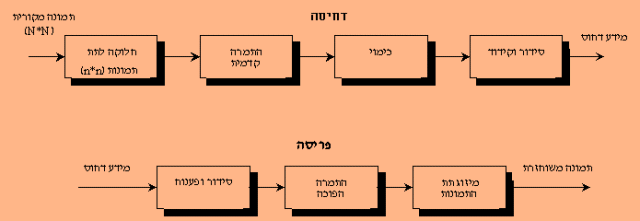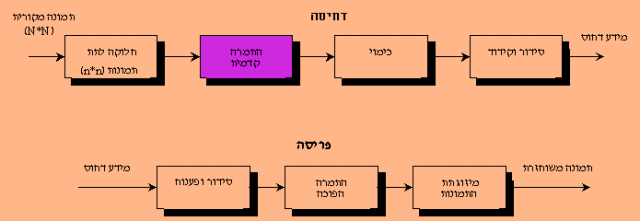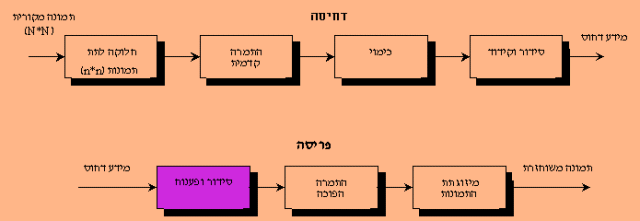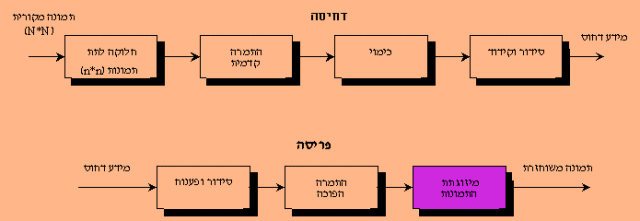
בשלב ראשון מחולקת התמונה, שגודלה N*N לתת תמונות בגודל n*n מטעמי יעילות חישובית
(ישנן אם כן (N/n)^2 תת תמונות כאלו).
על כל תמונה מתבצעת ההתמרה בנפרד. לאחר ההתמרה, מתקבל, עבור כל תת תמונה, מערך בגודל של n*n מקדמי התמרה, ומקדמי
התמרה של כל תת תמונה עוברים כימוי. מקדמי התדרים הגבוהים, הנושאים פחות מידע (ערכם נמוך), נזנחים (שלב זה נקרא קיצוץ), או
עוברים כימוי גס בלבד. חסרונם של מקדמים אלו לא יהיה בעל השפעה רבה על איכות התמונה בעת הפריסה. בשלב האחרון של הדחיסה, מקדמי ההתמרה,
שנותרו אחרי הכימוי, עוברים קידוד, בד"כ לקוד בעל אורך משתנה, כמו קוד הופמן. מידע מקודד זה הוא
התמונה הדחוסה. החלוקה לתת תמונות
גודלה של תת תמונה, n, נקבע עפ"י שני שיקולים: יעילות ומורכבות חישובית וטיב הדחיסה המתקבלת (איכותה וכמותה). ראשית, ניתן לייעל
מאד את חישוב ההתמרה, כאשר n מהווה חזקה שלמה של 2, ולכן תמיד בוחרים
....,4, 2 = n. שנית, ככל שתמונה מחולקת לתת תמונות קטנות יותר, גדלה מהירות החישוב של ההתמרה הכוללת.
למשל, מספר פעולות הכפל שנדרש לחישוב התמרת פוריה דו ממדית, של מערך נקודות בגודל n*n הוא n^2log2n.
ניתן איפה לראות, כי ע"י חלוקת התמונה בגודל N*N לתת תמונות בגודל n*n, מספר הפעולות הנדרשות קטן פי
ביצוע ההתמרה
ישנן כמה התמרות שנמצאו מתאימות לדחיסת תמונה. התמרות שונות משיגות רמה שונה של אי תלות בין מקדמיהן, ומאפשרות בכך דרגה שונה של דחיסה.
הבחירה בהתרמה מסוימת קשורה הן בשגיאת הפריסה המותרת והן במורכבות החישובית. 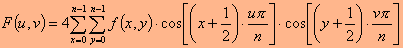 כאשר f(x,y) הם ערכי נקודות התמונה, F(u,v) הם ערכי נקודות ההתמרה (מקדמי ההתמרה), ו-n^2 מקדמי ההתמרה הללו מייצגים את רכיבי התדר המרחבי במערך תת התמונה הנדון. כל מקדם מתאים לתדר מרחבי דו ממדי אחר, כאשר u מציין את התדר המרחבי בכיוון x, ו-v את התדר המרחבי בכיוון y. כך למשל, המקדם עם תדר מרחבי אפס בשני הממדים, רכיב ה-DC, הוא המקדם הראשון במטריצת המקדמים, F(0,0). 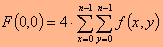 רכיב זה יחסי לממוצע כל ערכי הנקודות במערך התמונה הנדון, בגודל n*n. שאר המקדמים קרויים מקדמי AC. מקדמי ה-AC, הממוקמים בקרבת מקדם ה-DC, מתאימים למרכיבי התדר המרחבי הנמוך, ואילו הרחוקים ממנו הם מרכיבי התדר המרחבי הגבוה. מאחר שההשתנות בין נקודה לנקודה בתמונה היא בד"כ איטית, הרי המקדמים המשמעותיים של התמרת ה-DCT יהיו אלו המתאימים לתדירויות המרחביות הנמוכות, בסביבת הראשית (כלומר, בפינה השמאלית העליונה של מערך המקדמים). שאר המקדמים יהיו בעלי ערך אפס או קרוב לו. התמרת ה-DCT עצמה אינה גורמת לאיבוד מידע, כאשר מקדמיה מחושבים באופן מדויק. היא רק ממירה את אות התמונה לתחום שבו ניתן לדחוס אותו ביתר יעילות. כימוי: קיצוץ והקצאת סיביותלאחר שהתקבל מערך מקדמי ההתמרה עבור התת תמונה בגודל n*n, מתבצע הכימוי. מטרת שלב הכימוי היא להציג את מקדמי ההתמרה בדיוק, שלא יעלה על הנחוץ להשגת תמונה פרוסה באיכות הרצויה, ולהזניח מידע בלתי חשוב חזותית. הכימוי מורכב למשעה משני שלבים: קיצוץ מערך המקדמים (ע"י איפוס המקדמים הפחות חשובים), והקצאת סיביות למקדמים, שנבחרו (נותרו לאחר הקיצוץ). לעיתים קרובות משלבים יחד את שתי הפעולות, הקיצוץ והקצאת הסיביות. קיצוץ
בחירת המקדמים בשל הקיצוץ נעשית על פי שני קריטריונים. האחד - המקדמים נבחרים על פי הגודל שלהם, מתוך הנחה שככל שהמקדם גדול יותר
, יש בו יותר מידע. מעשית, מגדירים סף מסוים שהמקדמים הגדולים ממנו מכומים, והקטנים ממנו מאופסים. שיטה זו מכונה קידוד סף
(אם כי, למעשה מדובר בקיצוץ סף). בשיטה זו מספר הנבחרים ומיקומם במערך ההתמרה תלוי בתכונות תת התמונה, ועשוי להשתנות בין תת
תמונות שונות. קביעת הסף נעשית באחת מ-3 הדרכים:
על פי הקריטריון השני, המקדמים נבחרים לפי השונות שלהם על פני כלל התמונה. מעשית, מתקבל אזור של מקדמים נבחרים בסביבת הראשית
(כלומר בתדרים המרחביים הנמוכים). לכן, השיטה הזו נקראת קידוד אזורי (אם כי, מדובר בקיצוץ אזורי). שיטה זו מקובלת פחות משיטת
קידוד הסף, הן בגלל מספר הפעולות הגדול שנדרש לחישוב השונות בכל תמונה מחדש, והן מפני שהתוצאה המתקבלת טובה פחות מאשר בקידוד סף. הקצאת סיביות
את הכימוי ניתן לבצע בכמה דרכים: סידור וקידוד
את מערכי תת התמונות לאחר כימוי יש להפוך לרצף מסודר של סיביות, ואז לקודד באופן יעיל. ניתן לסדר את הסיביות בכמה דרכים. למשל, ניתן לקרוא את המערך שורה אחר שורה, או עמודה אחר עמודה. אולם הדרך המקובלת היא דרך בצורת זיג זג. בצורה כזו, המקדמים מסודרים על פי תדר מרחבי עולה, בד"כ משמעותו גודל יורד של המקדמים. לכל דרך יש יתרון לגבי קידוד יעיל. 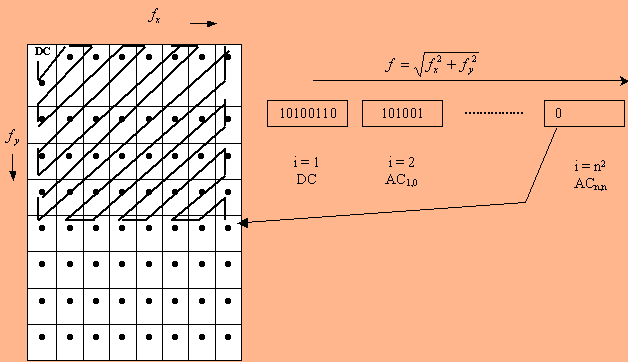 לאחר הסידור, סדרת הסיביות מקודדת לקוד בעל אורך משתנה, על מנת להגדיל עוד יותר את יעילות הדחיסה. ניתן לעשות זאת ע"י קידוד הופמן או RLE, או שילוב של שניהם. פריסה
בשלב הפריסה התמונה המקורית פרוסה מתוך התמונה הדחוסה. תחילה משוחזרים מקדמי ההתמרה בהתאם לקוד שנבחר וע"י כימוי הפוך. מקדמי ההתמרה המשוחזרים מסודרים בתת מערכים מסדר n*n, ועוברים התמרה הפוכה, DCT-1  כאשר (C(u,v היא ההתמרה ו-(f(x,y היא ההתמרה הפוכה והמקדמים (w(u), w(v ניתנים ע"י 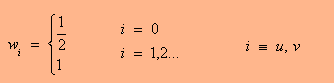
ללא הקיצוץ והכימוי של מערכי המקדמים, ניתן היה לפרוס את התמונה המקורית באופן מדויק. אולם, מאחר ששני צעדים אלה אינם הפיכים,
נוצר איבוד מידע בתהליך הדחיסה. ככל שרמת הדחיסה הנדרשת גבוהה יותר, גדלה מידת הקיצוץ (נבחרים פחות מקדמים), והכימוי נעשה גס יותר.
לכן, משקלו היחסי של איבר ב-DC הולך וגדל, וכתוצאה מכך תת התמונה נעשית אחידה יותר. כתוצאה מכך מתרחשות שתי
תופעות: מצד אחד, פרטי התמונה מטשטשים, ומצד שני, הדבר גורם לתמונה הפרוסה להיראות כמורכבת מריבועים (בגודל תת התמונות), דבר שפוגם
באופן ניכר באיכותה. "ריבועיות" זו בולטת בעיקר ביחסי דחיסה גבוהים מ-20:1 בערך. ככל שמידת הפירוט בתמונה המקורית
גבוהה יותר, המבנה הריבועי בולט ביחסי דחיסה נמוכים יותר. | ||||

|
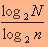 . החיסכון הזה לכשעצמו אינו גדול במיוחד, אולם הקטנת גודל המערך מקטינה
גם את מורכבות מערכת החישוב. לכך יש חשיבות במימוש רכיבי דחיסה מעשיים, בעיקר כאלו שאמורים לדחוס בזמן אמת.
. החיסכון הזה לכשעצמו אינו גדול במיוחד, אולם הקטנת גודל המערך מקטינה
גם את מורכבות מערכת החישוב. לכך יש חשיבות במימוש רכיבי דחיסה מעשיים, בעיקר כאלו שאמורים לדחוס בזמן אמת.






