סיווג שיטות לדחיסת תמונה
שיטות הדחיסה המקובלות מתחלקות באופן כללי ל-3 קבוצות עיקריות:
הראשונה, שיטת הדחיסה המשערכת, מנצלת את התלות בין ערכיהן של נקודות תמונה סמוכות.
תלות זו מבטאת את המידע העודף בתמונה (זה הניתן לדחיסה), שכן היא מאפשרת לשערך את ערך הנקודה בתמונה, בהסתמך על ערכי נקודות
התמונה שבסביבתה. אז אין צורך לשמור על ערך כל נקודה בתמונה, אלא רק על האופן שבו ניתן לקבלו כתלות בסביבתו.
שיטת הדחיסה השנייה נקראת דחיסת פיקסל, ובה כל נקודה בתמונה עוברת עיבוד בנפרד,
בלא תלות בנקודות אחרות. במקרה זה, הקוד הניתן לערכים שונים של נקודות התמונה אינו בהכרח בעל אורך אחיד, דבר המאפשר ייצוג חסכוני.
בשתי השיטות הראשונות, הקידוד מתבצע ישירות על נקודות התמונה. בשיטה השלישית, הנקראת דחיסת התמרה, דחיסת התמונה נעשית באופן בלתי ישיר. תחילה מבוצעת פעולה מתמטית על התמונה, המתמירה את מערך התמונה למערך אחר, מתאים יותר לדחיסה מאשר התמונה המקורית.
 דחיסת פיקסל
דחיסת פיקסל
הדרך הפשוטה ביותר לקידוד היא לתת לכל פיקסל ייצוג עם מספר סיביות זהה, יחסית לרמת הבהירות בו.
מקובל לייצג את רמות האפור ע"י 8 סיביות לתמונה שחור-לבן, או ע"י 8
סיביות לכל אחד משלושת הצבעים RGB בתמונה צבעונית. דרך אחרת היא ייצוג
ע"י סיבית בודדת, המשודרת בקצב גבוה. קידודים אלו, שבהם מספר הסיביות הוא אחיד לכל פיקסל, מכונים בשם הכללי קידודי
PCM. ישנן כיום שיטות חסכוניות יותר מקידוד זה.
 קידוד סטטיסטי
קידוד סטטיסטי
כאשר רמות הבהירות בתמונה אינן מפולגות באופן אחיד, הגיוני להשתמש בקוד בעל אורך משתנה. חיסכון בייצוג יושג,
אם הערכים השכיחים יותר ייוצגו ע"י מספר מועט של סיביות, ואילו הערכים הפחות שכיחים ייוצגו ע"י מספר רב יותר של סיביות.
קידוד מעין זה מכונה קידוד סטטיסטי, או קידוד אנטרופיה.
כאשר באים ליישם הגיון זה, יש להבחין בשני מקרים: התמונה הרגילה (תמונת רמות אפור) ותמונת התדרים המרחביים שלה.
בתמונה הרגילה היסטוגרמת רמות האפור אינה אחידה בד"כ, אולם ההיסטוגרמה הממוצעת לטווח ארוך (כלומר, אם נבחן מספר גדול של תמונות) היא, בקירוב טוב, אחידה. במילים אחרות, לא ניתן לייחס שכיחות גבוהה לרמות אפור מסוימות. לכן, קידוד סטטיסטי אינו יעיל כשמדובר בתמונה עצמה. אולם, בתחום התדרים המרחביים המצב שונה לחלוטין. מאחר שרוב האנרגיה מרוכזת בתחום צר של תדרים נמוכים, פילוג ערכי הפיקסלים במערך ההתמרה, אינו אחיד כלל, באופן שיטתי: הערכים הגבוהים של מעט האיברים שבאזור התדרים הנמוכים, שכיחים הרבה פחות מן הערכים הנמוכים של הרוב המכריע של האיברים שמצויים מחוץ לאזור זה. לכן, קידוד סטטיסטי של מערך התמרה מתאימה יהיה יעיל מאד.
היבט מעשי אחר של שימוש בקוד סטטיסטי נוגע לאפשרות להפריד בין מילים עוקבות, ברצף הסיביות שמייצגות את התמונה המקודדת (מאחר ששוב אין כל המילים בעלות אותו אורך).
תכונה הכרחית לכל קוד שמילותיו אינן בעלות אורך אחיד היא, ששום מילת קוד אינה מהווה קידומת של מילת קוד אחרת. כלומר, מילת קוד לא יכולה להוות את החלק הראשון (משמאל) של מילת קוד אחרת.
הסיבה לכך ברורה. כאשר מילות הקוד נשמרות (או נשלחות) זו אחר זו, חייבים לדעת היכן מסתיימת מילת קוד אחת ומתחילה השנייה. אם כל מילות הקוד הן בעלות אורך זהה, ההפרדה ביניהן פשוטה. אם, למשל,
אורכה של כל מילת קוד הוא 8 סיביות, ההפרדה בין מילות קוד עוקבות נעשית ע"י מנייה. בכל פעם שמניית מספר הסיביות
הגיעה ל-8, סימן שתמה מילת קוד אחת ומתחילה הבאה אחריה.
דרך הפרדה זו אינה אפשרית כאשר מילות הקוד הן בעלות אורך שונה. אז התנאי ההכרחי להפרדה בין מילות קוד עוקבות הוא שאין מילת
קוד המהווה קידומת למילת קוד אחרת.
 קידוד הופמן
קידוד הופמן
אלגוריתם הקידוד של הופמן (שהוצע בשנת 1962)
מאפשר לייצג באופן חסכוני את רמות הבהירות השונות, על פי מידת שכיחותן,
תוך קיום אילוץ ההפרדה בין מילות הקוד.
כבסיס ליצירת קוד הופמן של תמונה מסוימת (שמיוצגת על ידי סדרת מספרי בהירויות הפיקסלים), נתונות השכיחויות של רמות הבהירות בתמונה.
אם נתון, למשל, שהשכיחות של רמת בהירות A היא 0.25, פירוש הדבר שרבע מנקודות התמונה הן בעלות ערך A.
תהליך יצירת קוד הופמן שקול לבניית עץ בינארי, אשר צמתיו הם רמות הבהירות השונות. בכל שלב בבניית העץ נוסף לו צומת חדש ע"י איחוד שני הצמתים בעלי השכיחות הנמוכה ביותר. השכיחות של הצומת החדש שווה לסכום השכיחויות של שני הצמתים שהתאחדו. אחרי ששני צמתים אוחדו, שוב אין מתייחסים לשכיחותיהן, אלא לשכיחת הצומת שנוצר כתוצאה מאיחודם (ואליו מתייחסים כאשר בוחרים את שני הצמתים בעלי השכיחות הנמוכה ביותר בשלב הבא).
בניית עץ הקוד של הופמן מסתיימת אחרי שכל הצמתים אוחדו. הקוד עצמו מתקבל מן העץ על ידי הצבת '0'
ו-'1' לשתי התפצלויות מכל צומת. אין חשיבות לסדר ההצבה, כלומר אפשר להציב '1'
להתפצלות הימנית ו-'0' לשמאלית, או להפך (אך בכל מקרה יתקבל קוד שונה).
הקוד עבור רמת בהירות A הוא אוסף הסיביות על הענפים המחברים את שורש העץ אל הצומת של
הרמה A. חשוב להדגיש שקוד הופמן אינו יחיד, וקיימות אפשרויות שונות לבנות אותו עבור תמונה נתונה
(כלומר ישנם עצים אפשריים שונים).
היעילות של קידוד הופמן לסדרת מספרים נתונה (כלומר, יחס הדחיסה שניתן לקבל) גדלה ככל שמספר הרמות בסדרה המקורית גדול יותר,
וככל שהבדלי השכיחויות בין הרמות השונות גדולים יותר.
ולהפך: בסדרה שבה הרמות השונות מופיעות בשכיחויות דומות, אין טעם לבצע קידוד הופמן, משום שלא תתקבל דחיסה משמעותית, ויתרה מכך -
לעיתים כמות הסיביות הדרושה לייצוג הסדרה אף תגדל.
 קידוד Run-length (RLE)
קידוד Run-length (RLE)
בשטחי תמונה, שבהם רמת הבהירות משתנה באופן מתון (תדירויות מרחביות נמוכות), יהיו קטעים רצופים שבהם ערכי הפיקסלים זהים. במקום לציין בייצוג מלא את כל ערכי הפיקסלים הזהים, די במקרה זה לציין את ערך הפיקסל הראשון בקבוצה, ואת מספר הפיקסלים העוקבים בעלי אותו ערך. קידוד כזה נקרא קידוד Run-Length (ובקיצור RLE).
הקידוד נעשה תוך סריקה אופקית של שורות התמונה, והוא מחליף את רצף הפיקסלים בשורה באוסף הזוגות
(g1, l1),
(g2, l2),...,(gk, lk),
כאשר gi מייצג את ערך הפיקסל הראשון בקבוצה, ו-li מציין את מספר הפיקסלים בעלי אורך זהה
הבאים בעקבותיו.
קוד RLE יעיל, למשל, בקידוד של מפות מזג אוויר או תמונות לווין של שטחים נרחבים. במקרים האלה, ניתן לצפות להשתנות
מתונה של רמות הבהירות ולאותה בהירות בקטעים שלמים.
השימוש בקידוד RLE יעיל במיוחד לתמונות בעלות שני ערכים (תמונה בינארית),
כמו תמונת פקסימיליה. במקרה זה, אין צורך לציין את ערך הפיקסל הראשון בכל קבוצת ערכים אלא רק לציין את ערך הנקודה הראשונה בכל שורה ואת
אורכי הקבוצות כלומר: g1, l1, l2, ...., lk. מייצוג זה ברור,
ש-l1 פיקסלים הם בעלי אורך g1 כלומר 1
או 0 , אחריהם יהיו l2 פיקסלים בעלי ערך הפוך (0 אם
g1 = 1, אם g1 = 0 אז 1),
קבוצה באורך g3 פיקסלים בעלי אורך זהה ל-g1, וכן הלאה.
ברור גם, כי לתמונה לא בינארית, הכוללת שטחים בעלי תדר מרחבי גבוה (השתנות מהירה של רמות הבהירות), קידוד RLE
אינו יעיל. אם, לדוגמה, הבהירות משתנה עם כל פיקסל לאורך השורה, יידרש מספר סיביות כפול לייצוגה בעזרת קוד RLE,
לעומת ייצוג כל פיקסל בנפרד. זאת משום שבנוסף לערך הפיקסל, מצוין לידו גם אורך הקבוצה, שבמקרה זה הוא 1.
לבסוף, ניתן להעביר תמונה דחוסה בקידוד RLE, בקוד הבנוי ממילים בעלות אורך אחיד
(PCM) או ממילים בעלות אורך משתנה
(למשל, בקידוד הופמן). האפשרות השנייה יותר יעילה בד"כ, משום שנוסף בה שלב שני של דחיסה.
 דחיסה משערכת
דחיסה משערכת
במרבית התמונות קיים מתאם מרחבי גבוה בין ערכי נקודות סמוכות בתמונה. מעברים חדים מוגבלים לקווי
גבול בין חלקים שונים בתמונה. לכן, הערך של כל נקודה בתמונה קרוב בד"כ לערכי שכנותיה בתמונה. במילים אחרות, ההפרשים בין נקודה אחת
לשכנותיה הם בד"כ קטנים ביחס לערך הנקודה עצמה.
אפשר לנצל את התכונה הזו לדחיסה, ע"י ייצוג התמונה באמצעות ההפרשים בה, ולא באמצעות ערכי הנקודות (הצורה הרגילה לייצוג). בעת פריסת התמונה
הדחוסה, משערכים את ערכה של כל נקודה (כלומר, מנבאים את ערכה) מתוך ערכי אותן נקודות שכנות, שערכיהן כבר קבועים. שיטת הדחיסה הזו נקראת
דחיסה משערכת.
הדרך הפשוטה והמהירה ביותר לדחוס בשיטה זו היא לשערך כל נקודה עפ"י ההפרש בינה לבין קודמתה. דחיסה כזו נקראת דחיסת PCM הפרשי, או דחיסת DPCM.
מאחר שבממוצע ערכי ההפרשים קטנים בהרבה מן הערכים של נקודות התמונה, נדרשות פחות רמות לייצוג התמונה ע"י הפרשים, ולכן - גם מספר מועט יותר של סיביות. לכן, במקום לשמור (או לשדר) את ערכי הנקודות עצמן, עדיף לשמור (או לשדר) את ערכי ההפרש בין נקודות סמוכות. הדרך הפשוטה ביותר לעשות זאת היא בעזרת חישוב ההפרש בתמונה המקורית בין כל נקודה לקודמתה, כלומר
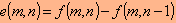
כאשר

הוא ערך הנקודה, m ו- n הם מספרי השורה והעמודה ו- e הוא ערך ההפרש. במקרה כזה ערכי הנקודות בתמונה המשוערכת (או הפרוסה) - שנסמנן ע"י
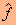
בשורה מסוימת, m , יתקבלו כך:
וכן הלאה.
פריסה מדויקת של ערכי הנקודות בתמונה, מתוך ערכי ההפרש e, מותנה בייצוג מלא ומדויק של ערכי e.
מאחר שתחום הערכים האפשרי של e הוא
[255 -255], כלומר כפול מתחום ערכי נקודות התמונה, לא רק שאין דחיסה,
אלא ההפך מכך: יש לייצג את e ע"י 9 סיביות במקום 8.
כדי לקבל דחיסה, יש לכמות את ההפרש e באמצעות מספר קטן ככל האפשר של סיביות.
את ההפרש המכומה נסמן ע"י 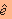 . נניח, למשל, שמכמים את ההפרש באמצעות
3 סיביות (ובכך מאפשרים את דחיסת התמונה ביחס 8:3) אופן הקצאת הסיביות הללו לכימוי ההפרש
הוא בעל חשיבות רבה: ראשית, יש לחלק את התחום לשניים, מחצית חיובית ומחצית שלילית. שנית, יש לקבוע את אופן הכימוי: אם ,למשל,
כל רמת אפור בייצוג ההפרשי זהה לרמת אפור בתמונה המקורית, אזי ההפרש בין זוג נקודות סמוכות
מוגבל לתחום [4,-4] (בעזרת 3 סיביות ניתן לייצג 8 ערכים). מגבלה זו יוצרת בעיה
במקומות שבהם מעברי בהירות חדים בתמונה, שבהם ההפרש המכומה רווי ואינו מייצג את מלוא השינוי האמיתי בתמונה.
. נניח, למשל, שמכמים את ההפרש באמצעות
3 סיביות (ובכך מאפשרים את דחיסת התמונה ביחס 8:3) אופן הקצאת הסיביות הללו לכימוי ההפרש
הוא בעל חשיבות רבה: ראשית, יש לחלק את התחום לשניים, מחצית חיובית ומחצית שלילית. שנית, יש לקבוע את אופן הכימוי: אם ,למשל,
כל רמת אפור בייצוג ההפרשי זהה לרמת אפור בתמונה המקורית, אזי ההפרש בין זוג נקודות סמוכות
מוגבל לתחום [4,-4] (בעזרת 3 סיביות ניתן לייצג 8 ערכים). מגבלה זו יוצרת בעיה
במקומות שבהם מעברי בהירות חדים בתמונה, שבהם ההפרש המכומה רווי ואינו מייצג את מלוא השינוי האמיתי בתמונה.
ניתן להתגבר על בעיה זו ע"י כימוי גס יותר של ההפרשים או ע"י יצירת אי אחידות בקצה התחום, שתאפשר קפיצות גדולות יחסית.
אולם, גם שיפור הכימוי מהווה פתרון חלקי בלבד. אם, למשל, מתרחשת קפיצת מדרגה של 50 רמות אפור בנקודה מסוימת,
הרי גם כימוי לא אחיד לא יעזור. לכן משנים את אופן חישוב ההפרש: במקום לחשבו בין שתי נקודות עוקבות בתמונה המקורית, מחשבים בכל
רגע את ההפרש בין הערך האמיתי של כל נקודה בתמונה המקורית לבין ערך הנקודה הקודמת בשורה, כפי שהוא אמור להתקבל בתמונה המשוערכת
(מחישוב ההפרשים). להלן מתואר תרשים של המערכת:

מערכת לדחיסה ופריסה בשיטת DPCM. סימול ה"כובע" על ערך התמונה f מייצג ערך משוערך
 דחיסת התמרה
דחיסת התמרה
דחיסת התמרה שונה מהשיטות שתיארנו עד כה בכך, שהדחיסה שוב אינה מתבצעת על התמונה עצמה, אלא על התמרה שלה. הרעיון בבסיס דחיסת ההתמרה הוא שבהתמרת התמונה, פילוג הערכים עשוי להיות מתאים יותר לדחיסה, מאשר בתמונה עצמה.
אחת הסיבות העיקריות למיותרות בתמונה היא המתאם המרחבי הגבוה, שמאפשר לשערך ערך בנקודה על סמך ערכים בסביבתה. לאחר התמרה לתחום התדר המרחבי, המתאם הגבוה מתבטא בכך שרוב רובו של במידע החזותי מרוכז למספר קטן יחסית של מקדמים (כלומר נקודות התמרה), באזור התדרים הנמוכים. דוגמה קיצונית לכך היא תמונה בעלת בהירות אחידה לחלוטין: לאחר התמרה ניתן לתארה באופן מדויק ומלא ע"י נקודת התמרה אחת בלבד (של התדר המרחבי אפס), במקום ע"י N*N נקודות בתמונה עצמה.
במרבית התמונות התיאור כמובן מורכב יותר, אולם, כאמור, רוב המידע מרוכז בתדרים הנמוכים, שמקדמיהם גדולים יחסית למקדמי התדרים הגבוהים. נוסף לכך, רגישות העין בתדרים הגבוהים היא נמוכה יחסית. כתוצאה משתי עובדות אלה, ניתן לכמות את מקדמי ההתמרה כתלות בתדר המרחבי שהם מייצגים: ככל שהתדר גבוה יותר, הכימוי יכול להיות גס יותר. בכך טמון רווח גדול מבחינת הדחיסה, משום שאת רוב רובן של נקודות ההתמרה ניתן לכמות באופן גס, או לאפסן לחלוטין (כלומר, להתעלם מהן).
יש להדגיש, כי בכל דחיסות ההתמרה, הדחיסה המתקבלת לא מן ההתמרה עצמה (שכמות המידע הגולמי בה זהה לזו שבתמונה), אלא מכימוי ומקידוד מקדמי ההתמרה.
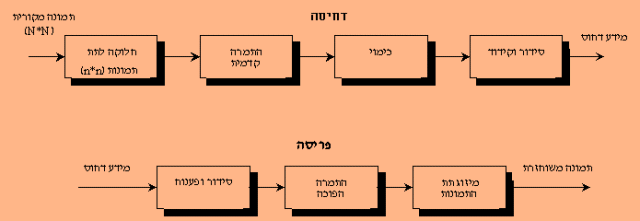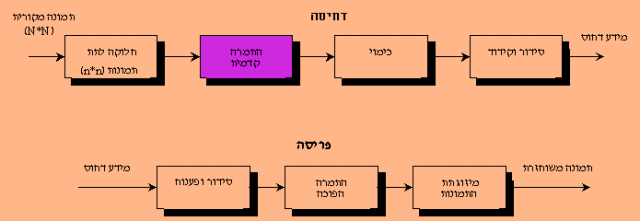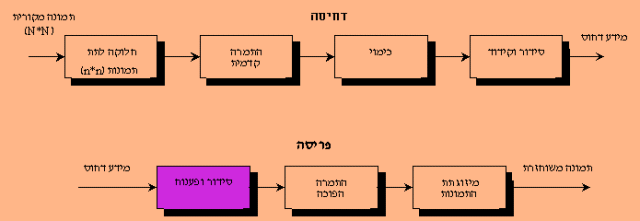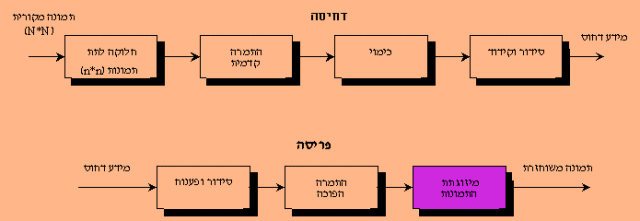
בשלב ראשון מחולקת התמונה, שגודלה N*N לתת תמונות בגודל n*n מטעמי יעילות חישובית
(ישנן אם כן (N/n)^2 תת תמונות כאלו).
על כל תמונה מתבצעת ההתמרה בנפרד. לאחר ההתמרה, מתקבל, עבור כל תת תמונה, מערך בגודל של n*n מקדמי התמרה, ומקדמי
התמרה של כל תת תמונה עוברים כימוי. מקדמי התדרים הגבוהים, הנושאים פחות מידע (ערכם נמוך), נזנחים (שלב זה נקרא קיצוץ), או
עוברים כימוי גס בלבד. חסרונם של מקדמים אלו לא יהיה בעל השפעה רבה על איכות התמונה בעת הפריסה. בשלב האחרון של הדחיסה, מקדמי ההתמרה,
שנותרו אחרי הכימוי, עוברים קידוד, בד"כ לקוד בעל אורך משתנה, כמו קוד הופמן. מידע מקודד זה הוא
התמונה הדחוסה.
בשלב הפריסה, מקדמי ההתמרה המקודדים עוברים תהליך הפוך. ראשית, על סמך אותה טבלה ששימשה לקידוד המקדמים, מתקבלים הערכים
שלפני הקידוד מתוך הערכים המקודדים. מקדמי ההתמרה שלאחר כימוי עוברים אז כימוי הפוך לשם קבלת מקדמי ההתמרה המקוריים. תהליך
הכימוי אינו הפיך, ומקדמי ההתמרה שמתקבלים אחרי הכימוי ההפוך אינם פריסה מדויקת של מקדמי ההתמרה המקוריים. לבסוף מקדמי ההתמרה
המשוחזרים עוברים התמרה הפוכה, לקבלת התת תמונה המקורית. דחיסת ההתמרה אינה משתמרת בשל תהליך הכימוי שאינו הפיך.
 החלוקה לתת תמונות
החלוקה לתת תמונות
גודלה של תת תמונה, n, נקבע עפ"י שני שיקולים: יעילות ומורכבות חישובית וטיב הדחיסה המתקבלת (איכותה וכמותה). ראשית, ניתן לייעל
מאד את חישוב ההתמרה, כאשר n מהווה חזקה שלמה של 2, ולכן תמיד בוחרים
....,4, 2 = n. שנית, ככל שתמונה מחולקת לתת תמונות קטנות יותר, גדלה מהירות החישוב של ההתמרה הכוללת.
למשל, מספר פעולות הכפל שנדרש לחישוב התמרת פוריה דו ממדית, של מערך נקודות בגודל n*n הוא n^2log2n.
ניתן איפה לראות, כי ע"י חלוקת התמונה בגודל N*N לתת תמונות בגודל n*n, מספר הפעולות הנדרשות קטן פי
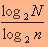 . החיסכון הזה לכשעצמו אינו גדול במיוחד, אולם הקטנת גודל המערך מקטינה
גם את מורכבות מערכת החישוב. לכך יש חשיבות במימוש רכיבי דחיסה מעשיים, בעיקר כאלו שאמורים לדחוס בזמן אמת.
. החיסכון הזה לכשעצמו אינו גדול במיוחד, אולם הקטנת גודל המערך מקטינה
גם את מורכבות מערכת החישוב. לכך יש חשיבות במימוש רכיבי דחיסה מעשיים, בעיקר כאלו שאמורים לדחוס בזמן אמת.
טיב הדחיסה נקבע ע"י שני גורמים: יחס הדחיסה המתקבל ושגיאת הפריסה המתקבלת. כללית,
ככל שיחס הדחיסה גדול יותר, גדלה גם שגיאת הפריסה. הקשר בין יחס הדחיסה לשגיאת הפריסה תלוי בגודל תת התמונה. אינטואיטיבית ברור,
שככל ששוברים את התמונה לתת תמונות קטנות יותר, מידע רב יותר הולך לאיבוד בתפרים שבין תת תמונות שכנות, ולכן שגיאת הפריסה גדלה.
ניתן להראות, כי עבור שגיאת פריסה נתונה, יחס הדחיסה האפשרי עבור תת תמונות של 16 * 16 גדול פי 2
ויותר מזה המתקבל עבור תת תמונות של 2 * 2. במילים אחרות, הדחיסה משתפרת ככל שתת התמונות גדולות יותר.
דבר זה אינו מפתיע.
מעשית, כפשרה בין הדרישה ליעילות חישובית לבין הדרישה לגבי טיב הדחיסה, מחלקים בד"כ את התמונה לתת תמונות של 16 * 16
או 8 * 8.
 ביצוע ההתמרה
ביצוע ההתמרה
ישנן כמה התמרות שנמצאו מתאימות לדחיסת תמונה. התמרות שונות משיגות רמה שונה של אי תלות בין מקדמיהן, ומאפשרות בכך דרגה שונה של דחיסה.
הבחירה בהתרמה מסוימת קשורה הן בשגיאת הפריסה המותרת והן במורכבות החישובית.
ההתמרה השימושית ביותר לדחיסה היא התמרת קוסינוס הדיסקרטית (DCT). ההתמרה האופטימלית היא זו המרכזת את
מירב המידע למספר קטן ביותר של מקדמי ההתמרה. המשמעות היא שבמקרה כזה, כאשר מבצעים כימוי במידה נתונה (למשל, מסלקים אחוז נתון
מן המקדמים בעלי הערכים הנמוכים ביותר), שגיאת הפריסה תהיה מינימלית. מבחינה זו נמצאה התמרת הקוסינוס מתאימה יותר מהתמרות אחרות
(כולל התמרת פוריה). למרות שאינה האופטימלית האפשרית, היא משמשת ברוב מערכות הדחיסה הקיימות, מפני שהיא ממזגת בין יכולת דחיסה
ובין סיבוכיות חישובית סבירה. לשם השוואה, כאשר מחלקים את התמונה לתת תמונות של 8 * 8, מסלקים
75% ממקדמי התמונה ומשחזרים, שגיאת הפריסה בהתמרת DCT תהיה כמחצית מזו שתתקבל בהתמרת פוריה. מבחינת מורכבות החישוב, שתי ההתמרות דומות.
התמרת קוסינוס ממירה תמונה בגודל n*n (תת תמונה) למערך מקדמי DCT, גם הוא בגודל n*n, על פי המשוואה:
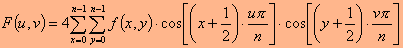
כאשר f(x,y) הם ערכי נקודות התמונה, F(u,v) הם ערכי נקודות ההתמרה (מקדמי ההתמרה),
ו-n^2 מקדמי ההתמרה הללו מייצגים את רכיבי התדר המרחבי במערך תת התמונה הנדון. כל מקדם מתאים לתדר מרחבי דו ממדי אחר,
כאשר u מציין את התדר המרחבי בכיוון x, ו-v את התדר המרחבי בכיוון y. כך למשל, המקדם עם תדר מרחבי אפס בשני הממדים,
רכיב ה-DC, הוא המקדם הראשון במטריצת המקדמים, F(0,0).
רכיב זה יחסי לממוצע כל ערכי הנקודות במערך התמונה הנדון, בגודל n*n. שאר המקדמים קרויים מקדמי AC. מקדמי
ה-AC, הממוקמים בקרבת מקדם ה-DC, מתאימים למרכיבי התדר המרחבי הנמוך, ואילו הרחוקים
ממנו הם מרכיבי התדר המרחבי הגבוה. מאחר שההשתנות בין נקודה לנקודה בתמונה היא בד"כ איטית, הרי המקדמים המשמעותיים של
התמרת ה-DCT יהיו אלו המתאימים לתדירויות המרחביות הנמוכות, בסביבת הראשית (כלומר, בפינה השמאלית
העליונה של מערך המקדמים). שאר המקדמים יהיו בעלי ערך אפס או קרוב לו. התמרת ה-DCT עצמה אינה גורמת
לאיבוד מידע, כאשר מקדמיה מחושבים באופן מדויק. היא רק ממירה את אות התמונה לתחום שבו ניתן לדחוס אותו ביתר יעילות.

כימוי: קיצוץ והקצאת סיביות
לאחר שהתקבל מערך מקדמי ההתמרה עבור התת תמונה בגודל n*n, מתבצע הכימוי. מטרת שלב הכימוי היא להציג את מקדמי ההתמרה בדיוק,
שלא יעלה על הנחוץ להשגת תמונה פרוסה באיכות הרצויה, ולהזניח מידע בלתי חשוב חזותית.
הכימוי מורכב למשעה משני שלבים: קיצוץ מערך המקדמים (ע"י איפוס המקדמים הפחות חשובים), והקצאת סיביות למקדמים, שנבחרו
(נותרו לאחר הקיצוץ). לעיתים קרובות משלבים יחד את שתי הפעולות, הקיצוץ והקצאת הסיביות.

קיצוץ
בחירת המקדמים בשל הקיצוץ נעשית על פי שני קריטריונים. האחד - המקדמים נבחרים על פי הגודל שלהם, מתוך הנחה שככל שהמקדם גדול יותר
, יש בו יותר מידע. מעשית, מגדירים סף מסוים שהמקדמים הגדולים ממנו מכומים, והקטנים ממנו מאופסים. שיטה זו מכונה קידוד סף
(אם כי, למעשה מדובר בקיצוץ סף). בשיטה זו מספר הנבחרים ומיקומם במערך ההתמרה תלוי בתכונות תת התמונה, ועשוי להשתנות בין תת
תמונות שונות. קביעת הסף נעשית באחת מ-3 הדרכים:
- סף קבוע על פני כל התמונה - במקרה כזה, מספר המקדמים הנבחרים בכל תת תמונה אינו אחיד.
- בחירת מספר מקדמים אחיד בכל תת התמונות - במקרה כזה, הסף אינו זהה לכל תת התמונות.
- הסף תלוי במיקום המקדם במערך המקדמים - במקרה כזה, הסף נקבע על פי תכונות העין ותכולת המידע בתמונה.
הוא נמוך בתדרים הנמוכים, וגבוה בתדרים הגבוהים. הסף משמש כרמת כימוי בתמונה. שיטה זו שימושית מאד כיום.
על פי הקריטריון השני, המקדמים נבחרים לפי השונות שלהם על פני כלל התמונה. מעשית, מתקבל אזור של מקדמים נבחרים בסביבת הראשית
(כלומר בתדרים המרחביים הנמוכים). לכן, השיטה הזו נקראת קידוד אזורי (אם כי, מדובר בקיצוץ אזורי). שיטה זו מקובלת פחות משיטת
קידוד הסף, הן בגלל מספר הפעולות הגדול שנדרש לחישוב השונות בכל תמונה מחדש, והן מפני שהתוצאה המתקבלת טובה פחות מאשר בקידוד סף.
בשני הקריטריונים המקדמים הנבחרים מצויים בסביבת הראשית, כלומר בתדרים המרחביים הנמוכים, שבהם טמון רוב המידע. אולם, בעוד שבכימוי
אזורי נוצר בד"כ רצף סביב הראשית, הרי בכימוי סף - שבו כל תת תמונה מכומה בנפרד - ייתכן שיהיו מקדמים חריגים בתת תמונות מסוימות.
מספר המקדמים הנבחר מן ההתמרה של כל תת תמונה משתנה בהתאם לשגיאה המותרת בפריסה. על פי שני הקריטריונים שנידונו לעיל, מקובל
לבחור כמייצגים 10%-15% מן המקדמים (ולהתעלם מן השאר). זה שקול לדחיסה ביחס של 10:1 ו-7:1, בהתאמה.

הקצאת סיביות
את הכימוי ניתן לבצע בכמה דרכים:
א. כימוי אחיד - של כל המקדמים הנבחרים, לרוב ל-8 סיביות.
ב. כימוי אזורי הדרגתי - מספר סיביות הכימוי קטן ככל שמתרחקים מן הראשית, ונוצרות מעין "חגורות כימוי".
שתי הדרכים האלה משתמשות בקידוד אזורי.
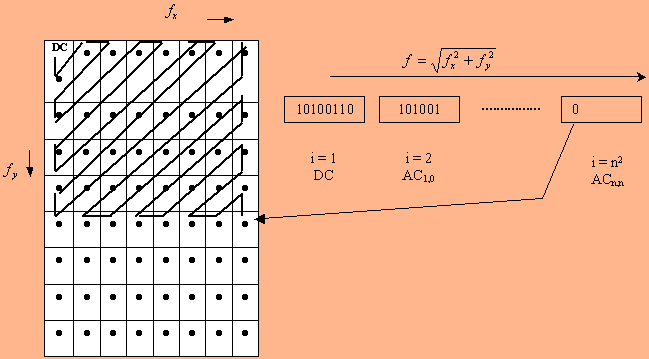
סידור וקידוד
את מערכי תת התמונות לאחר כימוי יש להפוך לרצף מסודר של סיביות, ואז לקודד באופן יעיל. ניתן לסדר את הסיביות בכמה דרכים. למשל, ניתן לקרוא את המערך שורה אחר שורה, או עמודה אחר עמודה. אולם הדרך המקובלת היא דרך בצורת זיג זג. בצורה כזו, המקדמים מסודרים על פי תדר מרחבי עולה, בד"כ משמעותו גודל יורד של המקדמים. לכל דרך יש יתרון לגבי קידוד יעיל.

לאחר הסידור, סדרת הסיביות מקודדת לקוד בעל אורך משתנה, על מנת להגדיל עוד יותר את יעילות הדחיסה. ניתן לעשות זאת ע"י
קידוד הופמן או
RLE, או שילוב של שניהם.

פריסה
בשלב הפריסה התמונה המקורית פרוסה מתוך התמונה הדחוסה. תחילה משוחזרים מקדמי ההתמרה בהתאם לקוד שנבחר וע"י כימוי הפוך. מקדמי ההתמרה המשוחזרים מסודרים בתת מערכים מסדר n*n, ועוברים התמרה הפוכה, DCT-1
(לעיתים מסלים את ההתמרה ההפוכה ב-DCTI), לפי המשוואה:
כאשר (C(u,v היא ההתמרה ו-(f(x,y היא ההתמרה הפוכה והמקדמים (w(u), w(v ניתנים ע"י
ללא הקיצוץ והכימוי של מערכי המקדמים, ניתן היה לפרוס את התמונה המקורית באופן מדויק. אולם, מאחר ששני צעדים אלה אינם הפיכים,
נוצר איבוד מידע בתהליך הדחיסה. ככל שרמת הדחיסה הנדרשת גבוהה יותר, גדלה מידת הקיצוץ (נבחרים פחות מקדמים), והכימוי נעשה גס יותר.
לכן, משקלו היחסי של איבר ב-DC הולך וגדל, וכתוצאה מכך תת התמונה נעשית אחידה יותר. כתוצאה מכך מתרחשות שתי
תופעות: מצד אחד, פרטי התמונה מטשטשים, ומצד שני, הדבר גורם לתמונה הפרוסה להיראות כמורכבת מריבועים (בגודל תת התמונות), דבר שפוגם
באופן ניכר באיכותה. "ריבועיות" זו בולטת בעיקר ביחסי דחיסה גבוהים מ-20:1 בערך. ככל שמידת הפירוט בתמונה המקורית
גבוהה יותר, המבנה הריבועי בולט ביחסי דחיסה נמוכים יותר.
בעזרת דחיסת ההתמרה (וקיצוץ וקידוד מתאימים), ניתן להגיע ליחסי דחיסה של עד 100:1. עם זאת, ביחס דחיסה כה גבוה
התמונה המתקבלת היא באיכות ירודה מאד, וניתן רק לקבל מושג כללי על תכולתה. איכות סבירה מתקבלת עד ליחס של 30:1 בערך
(תלוי בטיב ותכולת התמונה המקורית).





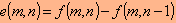
 הוא ערך הנקודה, m ו- n הם מספרי השורה והעמודה ו- e הוא ערך ההפרש. במקרה כזה ערכי הנקודות בתמונה המשוערכת (או הפרוסה) - שנסמנן ע"י
הוא ערך הנקודה, m ו- n הם מספרי השורה והעמודה ו- e הוא ערך ההפרש. במקרה כזה ערכי הנקודות בתמונה המשוערכת (או הפרוסה) - שנסמנן ע"י 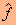 בשורה מסוימת, m , יתקבלו כך:
בשורה מסוימת, m , יתקבלו כך: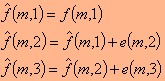


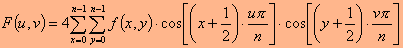
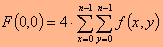

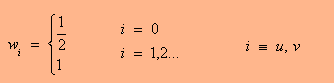

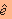 . נניח, למשל, שמכמים את ההפרש באמצעות
3 סיביות (ובכך מאפשרים את דחיסת התמונה ביחס 8:3) אופן הקצאת הסיביות הללו לכימוי ההפרש
הוא בעל חשיבות רבה: ראשית, יש לחלק את התחום לשניים, מחצית חיובית ומחצית שלילית. שנית, יש לקבוע את אופן הכימוי: אם ,למשל,
כל
. נניח, למשל, שמכמים את ההפרש באמצעות
3 סיביות (ובכך מאפשרים את דחיסת התמונה ביחס 8:3) אופן הקצאת הסיביות הללו לכימוי ההפרש
הוא בעל חשיבות רבה: ראשית, יש לחלק את התחום לשניים, מחצית חיובית ומחצית שלילית. שנית, יש לקבוע את אופן הכימוי: אם ,למשל,
כל 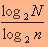 . החיסכון הזה לכשעצמו אינו גדול במיוחד, אולם הקטנת גודל המערך מקטינה
גם את מורכבות מערכת החישוב. לכך יש חשיבות במימוש רכיבי דחיסה מעשיים, בעיקר כאלו שאמורים לדחוס בזמן אמת.
. החיסכון הזה לכשעצמו אינו גדול במיוחד, אולם הקטנת גודל המערך מקטינה
גם את מורכבות מערכת החישוב. לכך יש חשיבות במימוש רכיבי דחיסה מעשיים, בעיקר כאלו שאמורים לדחוס בזמן אמת.






