|
|
|
| |
אתר ללימוד מקיף> פרק 14 - אי-דטרמיניסטיות
הנושאים בפרק זה:
14.1. תיאור של 'amb'
14.2. מימוש amb ב-Scheme
14.3. שימושי amb ב-Scheme
14.4. בעיות לוגיות
14.4.1. בעיית קלוטן (kalotan)
14.4.2. צביעת מפה
האופרטור האי-דטרמיניסטי של מכקרת'י amb הוא ותיק כמו lisp בעצמה, למרות שהוא אינו מוצג בה. amb מקבל אפס או יותר ביטויים, מבצע מעין בחירה אי-דטרמיניסטית ביניהם ומעדיף את הבחירות שייגרמו לתכנית להצליח באופן משמעותי. כאן נחקור שיבוץ של amb ב-Scheme שמבצע ברירה לעומק (dfs) של הבחירות אי-דטרמיניסטיות השונות, ומשתמש באופרטור הבקרה call/cc לבצע נסיגה (backtracking) עבור בחירה חלופית. התוצאה שתתקבל היא אסטרטגית נסיגה אלגנטית שתשמש לחקירת מרחבי בעיה בצורה ישירה ב-Scheme ללא צורך בעזרי שפה מורחבת. השילובים הנזכרים באסטרטגיות הממשיכות נועדו לממש Prolog - סוג של תכנות לוגי, אך מדובר בדבר פשוט יותר כיוון שהאופרטור המסופק הדומה מאד לאופרטור בוליאני ב-Scheme, אינו דורש הקשר מיוחד לשימושו ואינו מסתמך על תשתית לשונית כמו משתנים לוגיים ויוניפיקציות.

תיאור בר-שכנוע של amb והרבה דוגמאות שימוש נמצאים בספר ה-Scheme הראשון בחשיבותו SICP. באופן בלתי פורמלי, amb מקבלת אפס או יותר ביטויים ובאופן לא דטרמיניסטי מחזירה את הערך של אחד מהם. לפיכך,
(amb 1 2)
יוערך להיות 1 או 2.
amb שנקראת ללא ביטויים אינה מחזירה ערך ונחשב כי נכשלה (fail). לפיכך,
פרק 14 - אי-דטרמיניסטיות
הנושאים בפרק זה:
14.1. תיאור של 'amb'
14.2. מימוש amb ב-Scheme
14.3. שימושי amb ב-Scheme
14.4. בעיות לוגיות
14.4.1. בעיית קלוטן (kalotan)
14.4.2. צביעת מפה
האופרטור האי-דטרמיניסטי של מכקרת'י amb הוא ותיק כמו lisp בעצמה, למרות שהוא אינו מוצג בה. amb מקבל אפס או יותר ביטויים, מבצע מעין בחירה אי-דטרמיניסטית ביניהם ומעדיף את הבחירות שייגרמו לתכנית להצליח באופן משמעותי. כאן נחקור שיבוץ של amb ב-Scheme שמבצע ברירה לעומק (dfs) של הבחירות אי-דטרמיניסטיות השונות, ומשתמש באופרטור הבקרה call/cc לבצע נסיגה (backtracking) עבור בחירה חלופית. התוצאה שתתקבל היא אסטרטגית נסיגה אלגנטית שתשמש לחקירת מרחבי בעיה בצורה ישירה ב-Scheme ללא צורך בעזרי שפה מורחבת. השילובים הנזכרים באסטרטגיות הממשיכות נועדו לממש Prolog - סוג של תכנות לוגי, אך מדובר בדבר פשוט יותר כיוון שהאופרטור המסופק הדומה מאד לאופרטור בוליאני ב-Scheme, אינו דורש הקשר מיוחד לשימושו ואינו מסתמך על תשתית לשונית כמו משתנים לוגיים ויוניפיקציות.
14.1 תיאור של 'amb'
תיאור בר-שכנוע של amb והרבה דוגמאות שימוש נמצאים בספר ה-Scheme הראשון בחשיבותו SICP. באופן בלתי פורמלי, amb מקבלת אפס או יותר ביטויים ובאופן לא דטרמיניסטי מחזירה את הערך של אחד מהם. לפיכך,
(amb 1 2)
יוערך להיות 1 או 2.
amb שנקראת ללא ביטויים אינה מחזירה ערך ונחשב כי נכשלה (fail). לפיכך,
(amb) -->ERROR!!! amb tree exhausted |
(נדון בניסוחי הודעות השגיאה מאוחר יותר).
בייחוד, amb נדרשת להחזיר ערך אם לפחות אחד מתתי הביטויים שלה לא נכשל. לפיכך,
((amb 1 (amb)
ו-(amb (amb) 1)
שניהם מחזירים 1.
amb אינה יכולה פשוט להיות משוות לתת הביטוי הראשון שלה, מאחר ועליה להחזיר ערך שאינו כשלון אם זה בכלל אפשרי. בכל אופן, זה לא הכל: הדעה לגבי אי כשלון היא חזקה יותר מאשר סתם בחירה מקומית של תת ביטויי amb.amb צריכה יתר על כן להחזיר את ערך אי-הכישלון שגרם לתכנית כולה להצליח. כניב, ניתן לכנות את amb כ"אופרטור מלאכי".לדוגמא:
בייחוד, amb נדרשת להחזיר ערך אם לפחות אחד מתתי הביטויים שלה לא נכשל. לפיכך,
((amb 1 (amb)
ו-(amb (amb) 1)
שניהם מחזירים 1.
amb אינה יכולה פשוט להיות משוות לתת הביטוי הראשון שלה, מאחר ועליה להחזיר ערך שאינו כשלון אם זה בכלל אפשרי. בכל אופן, זה לא הכל: הדעה לגבי אי כשלון היא חזקה יותר מאשר סתם בחירה מקומית של תת ביטויי amb.amb צריכה יתר על כן להחזיר את ערך אי-הכישלון שגרם לתכנית כולה להצליח. כניב, ניתן לכנות את amb כ"אופרטור מלאכי".לדוגמא:
(amb #t #f) |
יחזיר או t# או f#, אך בתכנית-
(if (amb #t #f)
1
(amb))
|
ביטוי ה-amb הראשון חייב להחזיר t#. אם הוא יחזיר f#, ה-else יהיה זה שיבחר, מה שיגרום לתכנית כולה
להיכשל.

ראשית נגדיר מנגנון לקביעת הימשכות הכישלון הבסיסי:
14.2 מימוש 'amb' ב-Scheme
במימוש שלנו ל-amb, נעבור על ביטויי ה-amb משמאל לימין. כלומר, בהיבחר הביטוי הראשון, אם הוא יוביל לכישלון מקיף - ייבחר הביטוי הבא וכו'. amb המתרחש מאוחר יותר בזמן תזרים הבקרה של התכנית הוא זה המחפש חלופות לפני הנסיגה ל-amb הקודם. במילים אחרות, אנו מפעילים חיפוש לעומק בעץ ההחלטות של amb, וכל פעם שאנו עומדים מול כישלון, אנו נסוגים לצומת הקרובה ביותר בעץ שמציעה אפשרות בחירה נוספת. (תהליך זה נקרא נסיגה כרונולוגית).ראשית נגדיר מנגנון לקביעת הימשכות הכישלון הבסיסי:
(define amb-fail '*)
(define initialize-amb-fail
(lambda ()
(set! amb-fail
(lambda ()
(error "amb tree exhausted")))))
(initialize-amb-fail)
l
|
כאשר amb נכשל, הוא טוען את תחום ההימשכות של אותו הזמן ל-amb-fail. זה זמן ההימשכות שיופעל כאשר כל
האלטרנטיבות בעץ ההחלטות נוסו ונכשלו.
נגדיר את amb כמקרו המקבל מספר סתמי כלשהו של תתי ביטויים.
נגדיר את amb כמקרו המקבל מספר סתמי כלשהו של תתי ביטויים.
(define-macro amb
(lambda alts...
`(let ((+prev-amb-fail amb-fail))
(call/cc
(lambda (+sk)
,@(map (lambda (alt)
`(call/cc
(lambda (+fk)
(set! amb-fail
(lambda ()
(set! amb-fail +prev-amb-fail)
(+fk 'fail)))
(+sk ,alt))))
alts...)
(+prev-amb-fail))))))
|
קריאה ל-amb ראשית תאכסן ב-prev-amb-fail+ את ערך amb-fail הנוכחי בזמן הכניסה. זאת כיוון שמשתנה
ה-amb-fail מאותחל להימשכויות כשלונות שונים כמו מס' האלטרנטיבות השונות שאנו מנסים. אז אנו "לוכדים" את
כניסת ה-amb sk+, כך שכאשר ערך אחת האלטרנטיבות יהיה אי-כישלון, נוכל לצאת בקלות מ-amb.
מנסים כל אחת מאלטרנטיבות alt באופן סדרתי.
ראשית, אנו "לוכדים" את ההימשכות העכשווית fk+, "מכסים" אותה בפרוצדורה וטוענים amb-fail לפרוצדורה זו. האלטרנטיבה אז מוערכת כ-(sk alt+). אם alt מצליחה - ערכה יוזן ל-sk+, שייצא מייד מקריאת ה-amb. אם alt ייכשל, תתבצע קריאה ל-amb-fail. התפקיד הראשון של amb-fail הוא לטעון מחדש את amb-fail לערך שהיה לו בזמן הכניסה. אז נעשית פנייה אל הימשכות הכישלון fk+, שגורמת לאלטרנטיבה הבאה, אם קיימת, להיות מנוסה.
אם כל האלטרנטיבות נכשלות מתבצעת קריאה ל-amb-fail שבכניסת ה-amb, שאוכסן ב-prev-amb-fail+.

מנסים כל אחת מאלטרנטיבות alt באופן סדרתי.
ראשית, אנו "לוכדים" את ההימשכות העכשווית fk+, "מכסים" אותה בפרוצדורה וטוענים amb-fail לפרוצדורה זו. האלטרנטיבה אז מוערכת כ-(sk alt+). אם alt מצליחה - ערכה יוזן ל-sk+, שייצא מייד מקריאת ה-amb. אם alt ייכשל, תתבצע קריאה ל-amb-fail. התפקיד הראשון של amb-fail הוא לטעון מחדש את amb-fail לערך שהיה לו בזמן הכניסה. אז נעשית פנייה אל הימשכות הכישלון fk+, שגורמת לאלטרנטיבה הבאה, אם קיימת, להיות מנוסה.
אם כל האלטרנטיבות נכשלות מתבצעת קריאה ל-amb-fail שבכניסת ה-amb, שאוכסן ב-prev-amb-fail+.
14.3 שימושי amb ב-Scheme
כדי לבחור מספר בין 1 ל-10 היינו יכולים לומר
(amb 1 2 3 4 5 6 7 8 9 10) |
כדי להיות בטוחים, כתכנית, יוחזר לנו הערך 1, אך באופן עקרוני יכולנו לקבל את כל אחד מהמספרים המוזכרים.
הפרוצדורה number-between היא דרך מופשטת יותר לייצר מספרים ממס' נתון lo ועד מס' נתון hi (כולל קצוות):
הפרוצדורה number-between היא דרך מופשטת יותר לייצר מספרים ממס' נתון lo ועד מס' נתון hi (כולל קצוות):
(define number-between
(lambda (lo hi)
(let loop ((i lo))
(if (> i hi) (amb)
(amb i (loop (+ i 1)))))))
|
כך, הקריאה (number-between 1 6 ) תחזיר בהתחלה 1 .כשזה ייכשל, תתבצע לולאה וייוצר 2. כשזה ייכשל נקבל 3,
4 וכו' עד 6. אחרי 6, קריאה ללולאה עם ערך 7, שהוא גדול מ-6, תקרא ל-(amb), שייגרום לכישלון סופי. (זכור
כי (amb) בעצמה נותנת ערך כישלון). בנקודה זו, התכנית המכילה את הקריאה ל-(number-between 1 6 ) תבצע
נסיגה לקריאת ה-amb הקודמת כרונולוגית, ותנסה לספק את הקריאה באופן אחר.
הכישלון המובטח של (amb) יכול לשמש לתכנית assertions.
הכישלון המובטח של (amb) יכול לשמש לתכנית assertions.
(define assert
(lambda (pred)
(if (not pred) (amb))))
|
הקריאה (assert pred) עומדת על כך ש-pred יהיה בעל ערך אמת. אחרת, נקודת ההחלטה הנוכחית של amb - תיכשל.
להלן פרוצדורה המשתמשת ב-assert המייצרת ראשוני קטן או שווה לארגומנט שלה hi:
להלן פרוצדורה המשתמשת ב-assert המייצרת ראשוני קטן או שווה לארגומנט שלה hi:
(define gen-prime
(lambda (hi)
(let ((i (number-between 2 hi)))
(assert (prime? i))
i)))
|
הדבר נראה פשוט למדי, פרט לכך שכאשר קוראים לתכנית עם מספר כלשהו (נניח 20), היא תייצר את הפתרון הראשון
הטריוויאלי, כלומר ,2. אנו כמובן נרצה לקבל את כל הפתרונות, לא רק את הראשון. במקרה זה, נרצה את כל
המספרים הראשוניים הקטנים מ-20. דרך אחת לבצע זאת, היא לקרוא במפורש להמשך כשלון מייד לאחר שהתכנית ייצרה
את הפתרון הראשון.
לפיכך,
לפיכך,
(amb) => 3 |
זה מותיר אחריו המשך כשלון נוסף, שיכול להיקרא שוב עבור פתרון נוסף:
(amb) => 5 |
הבעיה בשיטה זו היא שתכנית בהתחלה נקראת מה-prompt של Scheme, ופתרונות מוצלחים מושגים גם ע"י קריאה
ל-amb ב-prompt של Scheme.
למעשה, אנו משתמשים בתכניות שונות (א"א לצפות כמה!), כדי להעביר מידע מתכנית קודמת לבא. במקום זאת, היינו מעונינים לקבל פתרונות אלו כערך המוחזר של תבנית כלשהי שנוכל לקרוא לה מכל הקשר בו אנו נמצאים. כדי לבצע זאת, הגדרנו את המקרו bag-of, שיחזיר את מופעי ההצלחות של הארגומנט הניתן לו. (אם הארגומנט אף פעם לא מצליח, bag-of יחזיר רשימה ריקה). לפיכך, נוכל לומר כי
למעשה, אנו משתמשים בתכניות שונות (א"א לצפות כמה!), כדי להעביר מידע מתכנית קודמת לבא. במקום זאת, היינו מעונינים לקבל פתרונות אלו כערך המוחזר של תבנית כלשהי שנוכל לקרוא לה מכל הקשר בו אנו נמצאים. כדי לבצע זאת, הגדרנו את המקרו bag-of, שיחזיר את מופעי ההצלחות של הארגומנט הניתן לו. (אם הארגומנט אף פעם לא מצליח, bag-of יחזיר רשימה ריקה). לפיכך, נוכל לומר כי
(bag-of (gen-prime 20)) |
יחזיר
(2 3 5 7 11 13 17 19) |
מקרו ה-bag-of מוגדר בצורה הבאה:
(define-macro bag-of
(lambda (e)
`(let ((+prev-amb-fail amb-fail)
(+results '()))
(if (call/cc
(lambda (+k)
(set! amb-fail (lambda () (+k #f)))
(let ((+v ,e))
(set! +results (cons +v +results))
(+k #t))))
(amb-fail))
(set! amb-fail +prev-amb-fail)
(reverse! +results))))
|
ראשית, bag-of שומר את הכניסה שלו amb-fail. הוא מגדיר מחדש את amb-fail להמשך מקומי k+ הנוצר בעזרת
בדיקת if. בתוך הבדיקה, הארגומנט e של bag-of מוערך. אם e מצליח - תוצאתו נאספת לרשימה הנקראת results+,
וההמשך המקומי נקרא עם הערך t#. זה גורם למשפט ה-if להצליח, תוך כדי ש-e מנסה שנית בנקודת הנסיגה הבאה.
כך מושגות תוצאות נוספות עבור e בדרך זו, וכולן נאספות לתוך results+. לבסוף, כש-e נכשל, תתבצע קריאה
ל-amb-fail הבסיסי, שזו בעצם קריאה פשוטה להמשך המקומי עם הערך f#. זה דוחף את השליטה אחרי ה-if.
נחזיר את amb-fail לערך שהיה לו קודם הכניסה, ונחזיר את results+. (ה-!reverse הוא פשוט כדי להפיק את
התוצאות באותו סדר בו הן יוצרו).

יום אחד, הוא פגש זוג קלוטני (דו-מיני) ואת בנם קיבי. וורף שאל את קיבי:
"האם אתה ילד?" קיבי ענה בקלוטנית, שאותה כמובן וורף לא הבין.
וורף פנה להורים (שיודעים אנגלית) לבקש הסברים. אחד מהם אמר: "קיבי אמר: אני בן". השני הוסיף: "קיבי היא בת. קיבי שיקרה".
קבע מהו המין של ההורים ושל קיבי.
הפתרון כולל הצגת קבוצת משתנים, השמת ערכי החלטות בתוכם ומניית המצבים שייתכנו כסדרה של ביטויי assert.
המשתנים: parent1 ,parent2 ו-kibi הם מין ההורים (לפי סדר הופעתם) ומינו של קיבי. kibi-self-desc הוא המין שקיבי טוען שהוא משתייך אליו (בקלוטנית).
?kibi-lied הוא משתנה בוליאני שאומר אם טענת קיבי לגבי מינו היתה שקר.
14.4 בעיות לוגיות
הכוח הטמון בחיפוש לעומק (dfs) יחד עם נסיגה (backtracking) נעשה בולט כשנדרשים לפתור בעיות לוגיות. בעיות אלו קשה לפתור באופן יוצא-דופן בצורה פרוצדורלית, אך יכולות להיפתר בתמציתיות ובהצהרתיות בעזרת amb, מבלי להחסיר ולו מעט מהקסם האופף בעיות אלו.14.4.1 בעיית קלוטן (kalotan)
הקלוטנים הם שבט עם הרגל משונה למדי. הגברים שבהם תמיד דוברי אמת. הנשים אינן אומרות שני משפטי אמת עוקבים או שני משפטי שקר עוקבים. אנתרופולוג (בואו ונקרא לו וורף) החל לחקור שבט זה. וורף עדיין לא יודע את שפת קלוטן.יום אחד, הוא פגש זוג קלוטני (דו-מיני) ואת בנם קיבי. וורף שאל את קיבי:
"האם אתה ילד?" קיבי ענה בקלוטנית, שאותה כמובן וורף לא הבין.
וורף פנה להורים (שיודעים אנגלית) לבקש הסברים. אחד מהם אמר: "קיבי אמר: אני בן". השני הוסיף: "קיבי היא בת. קיבי שיקרה".
קבע מהו המין של ההורים ושל קיבי.
הפתרון כולל הצגת קבוצת משתנים, השמת ערכי החלטות בתוכם ומניית המצבים שייתכנו כסדרה של ביטויי assert.
המשתנים: parent1 ,parent2 ו-kibi הם מין ההורים (לפי סדר הופעתם) ומינו של קיבי. kibi-self-desc הוא המין שקיבי טוען שהוא משתייך אליו (בקלוטנית).
?kibi-lied הוא משתנה בוליאני שאומר אם טענת קיבי לגבי מינו היתה שקר.
(define solve-kalotan-puzzle
(lambda ()
(let ((parent1 (amb 'm 'f))
(parent2 (amb 'm 'f))
(kibi (amb 'm 'f))
(kibi-self-desc (amb 'm 'f))
(kibi-lied? (amb #t #f)))
(assert
(distinct? (list parent1 parent2)))
(assert
(if (eqv? kibi 'm)
(not kibi-lied?)))
(assert
(if kibi-lied?
(xor
(and (eqv? kibi-self-desc 'm)
(eqv? kibi 'f))
(and (eqv? kibi-self-desc 'f)
(eqv? kibi 'm)))))
(assert
(if (not kibi-lied?)
(xor
(and (eqv? kibi-self-desc 'm)
(eqv? kibi 'm))
(and (eqv? kibi-self-desc 'f)
(eqv? kibi 'f)))))
(assert
(if (eqv? parent1 'm)
(and
(eqv? kibi-self-desc 'm)
(xor
(and (eqv? kibi 'f)
(eqv? kibi-lied? #f))
(and (eqv? kibi 'm)
(eqv? kibi-lied? #t))))))
(assert
(if (eqv? parent1 'f)
(and
(eqv? kibi 'f)
(eqv? kibi-lied? #t))))
(list parent1 parent2 kibi))))
|
הערה לגבי פרוצדורות העזר: הפרוצדורה ?distinct מחזירה אמת אם כל האלמנטים ברשימת הארגומנטים שלה נבדלים,
ושקר אחרת. הפרוצדורה xor מחזירה אמת אם רק אחד משני הארגומנטים שלה ערכו אמת ,ושקר אחרת.
הקלדת (solve-kalotan-puzzle) אכן תפתור את הבעייה.

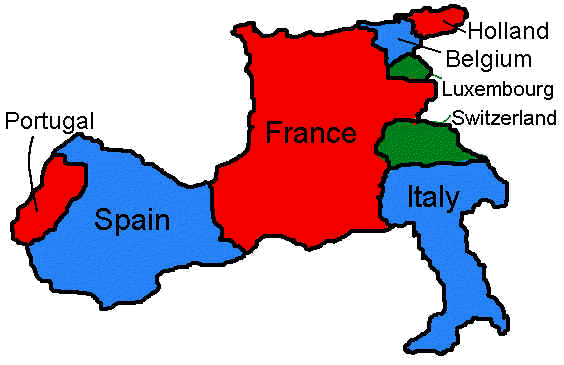
התכנית הבאה פותרת את בעיית צביעת מפה של אירופה המערבית. הבעיה והפתרון ב-prolog מוצגים ב-The art of prolog .(מאלף יהיה להשוות את פתרונינו עם הפתרון בספר).
הפרוצדורה choose-color מחזירה באופן אי-דטרמיניסטי אחד מארבעה צבעים:
הקלדת (solve-kalotan-puzzle) אכן תפתור את הבעייה.
14.4.2 צביעת מפה
במשך זמן מה היה ידוע הדבר (למרות שרק הוכח לאחרונה), שארבעה צבעים מספיקים לצבוע מפה יבשתית - כלומר, לצבוע את המדינות כך שנוכל להבחין בין שתי מדינות שכנות. הקצאת הצבעים ,למעשה, היא עדיין משימה לא קלה והתכנית הבאה מראה איך תכנות אי-דטרמיניסטי יכול לעזור.התכנית הבאה פותרת את בעיית צביעת מפה של אירופה המערבית. הבעיה והפתרון ב-prolog מוצגים ב-The art of prolog .(מאלף יהיה להשוות את פתרונינו עם הפתרון בספר).
הפרוצדורה choose-color מחזירה באופן אי-דטרמיניסטי אחד מארבעה צבעים:
(define choose-color
(lambda ()
(amb 'red 'yellow 'blue 'white)))
|
בפתרון שלנו, יצרנו לכל מדינה מבנה נתונים. מבנה הנתונים הוא רשימה בעלת שלושה אלמנטים: האלמנט הראשון
ברשימה הוא שם המדינה, האלמנט השני הוא הצבע המוקצה לה, והאלמנט השלישי הוא צבען של שכנותיה. שים לב כי
אנו משתמשים באות הראשונה של שם המדינה למשתנה הצבע.
לדוגמא, הרשימה עבור בלגיה תהיה
לדוגמא, הרשימה עבור בלגיה תהיה
(list `belgium b (list f h l g )) |
כיוון שלפי הצהרות בעיה זו - השכנות של בלגיה הן צרפת (f), הולנד (h), לוקסמבורג (l), וגרמניה (g).
ברגע שיצרנו רשימות לכל מדינה, אנו מבטאים את התנאי (היחיד!) שעליהן לקיים, דהיינו, שלשום מדינה לא יהיה צבע כמו שכנותיה. במילים אחרות, עבור כל מדינה, אסור לאלמנט השני להיות חבר ברשימה של האלמנט השלישי.
ברגע שיצרנו רשימות לכל מדינה, אנו מבטאים את התנאי (היחיד!) שעליהן לקיים, דהיינו, שלשום מדינה לא יהיה צבע כמו שכנותיה. במילים אחרות, עבור כל מדינה, אסור לאלמנט השני להיות חבר ברשימה של האלמנט השלישי.
(define color-europe
(lambda ()
;choose colors for each country
(let ((p (choose-color)) ;Portugal
(e (choose-color)) ;Spain
(f (choose-color)) ;France
(b (choose-color)) ;Belgium
(h (choose-color)) ;Holland
(g (choose-color)) ;Germany
(l (choose-color)) ;Luxemb
(i (choose-color)) ;Italy
(s (choose-color)) ;Switz
(a (choose-color)) ;Austria
)
;construct the adjacency list for
;each country: the 1st element is
;the name of the country; the 2nd
;element is its color; the 3rd
;element is the list of its
;neighbors' colors
(let ((portugal
(list 'portugal p
(list e)))
(spain
(list 'spain e
(list f p)))
(france
(list 'france f
(list e i s b g l)))
(belgium
(list 'belgium b
(list f h l g)))
(holland
(list 'holland h
(list b g)))
(germany
(list 'germany g
(list f a s h b l)))
(luxembourg
(list 'luxembourg l
(list f b g)))
(italy
(list 'italy i
(list f a s)))
(switzerland
(list 'switzerland s
(list f i a g)))
(austria
(list 'austria a
(list i s g))))
(let ((countries
(list portugal spain
france belgium
holland germany
luxembourg
italy switzerland
austria)))
;the color of a country
;should not be the color of
;any of its neighbors
(for-each
(lambda (c)
(assert
(not (memq (cadr c)
(caddr c)))))
countries)
;output the color
;assignment
(for-each
(lambda (c)
(display (car c))
(display " ")
(display (cadr c))
(newline))
countries))))))
|