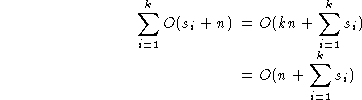7.5 מיון-בסיס
(radix sort)
מבנה נתונים
ואלגוריתמים
גישת
מיון-הסלים (bin sort) יכולה להיות מוכללת
בטכניקה הידועה כמיון-בסיס.
דוגמא:
נניח שיש לנו n ערכים שלמים בטווח של n²),0) הנדרשים למיון (עבור מיון סלים, m=n² ,
נקבל אלגוריתם של O(n+m)=O(n²)). נמיין אותם בשני שלבים:
1. בשימוש ב- n סלים, תוך מיקום ai
בסל n mod ai .
2. נחזור על ההליך עם השימוש ב-n סלים, תוך מיקום ai בסל (ai/n), ותוך הקפדה להוסיף כל פריט
לתחתית הסל.
התוצאה תהיה
רשימה ממוינת.
כדוגמא, נתייחס
לערכים השלמים הבאים:
4, 81, 16, 64, 49, 1, 25, 0, 9, 36
n
הוא 10, וכל המספרים הם בתחום (0,99). לאחר השלב הראשון נקבל:
|
סל |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
תוכן |
0 |
1 |
- |
- |
64 |
25 |
36 |
- |
- |
9 |
שים
לב כי בשלב זה מיקמנו כל פריט בסל שמספרו שווה לספרת האחדות של הערכים:
אם
נחזור שוב על ההליך נקבל:
|
סל |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
תוכן |
0 |
16 |
25 |
36 |
49 |
- |
64 |
- |
81 |
- |
בשלב
שני זה השתמשנו בספרת העשרות לצורך הקצאת הערכים לסלים, תוך הקפדה להוסיף כל פריט
לתחתית הסל.
ניתן
ליישם הליך זה למיון ערכים מכל גודל המיוצגים בכל בסיס אפשרי.
7.5.1 מיון-בסיס מוכלל
ניתן
לראות כי אין צורך בשימוש באותו בסיס בכל שלב. נניח שמפתח המיון הוא רצף של שדות,
שכל אחד מהם הוא בעל טווח תחום, כמו למשל כאשר המפתח הוא התאריך, תוך שימוש במבנה
הבא:
typedef struct t_date {
int day;
int month;
int year;
} date;
אם
הטווחים של day ושל month מוגבלים בדרך הרגילה,
והטווח של year מוגבל בתחום מסוים (למשל: 2000=year
>>1900), נוכל ליישם את אותו הליך, פרט לכך שנשתמש בכל שלב במספר סלים שונה.
בכל המקרים נמיין תחילה על פי "הספרה הכי פחות משמעותית"
("ספרה" - שדה עם טווח מוגבל), ונעבור הלאה לספרה המשמעותית הבאה, תוך
מיקום כל פריט לאחר הפריטים שכבר בסל, וכך הלאה.
נניח
שהמפתח לפריט הנדרש למיון הוא בעל k שדות, k-1..i=0| fi ,
ושלכל
fi יש si ערכים שונים, אזי ניתן לכתוב הליך של
מיון-בסיס מוכלל:
radixsort( A, n ) { for(i=0;i<k;i++) { for(j=0;j<si;j++) bin[j] = EMPTY; |
O(si) |
For(j=0;j<n;j++) { move Ai to the end of bin[Ai->fi] } |
O(n) |
For(j=0;j<si;j++) concatenate bin[j] onto the end of A; }} |
O(si) |
|
סך-הכל |
|
אם
למשל, המפתחות הם ערכים שלמים ב- (0, bk-1) ל-k
קבוע כלשהו, אז ניתן לראות את המפתחות כשלמים בעלי k
ספרות המיצגים בבסיס b .
כך,
si=b
לכל i וזמן הסיבוכיות הופך ל-
O(n+kb)
או O(n). תוצאה זו תלויה בהיות k קבוע.
אם
ניתן להגדיל את k עם n, אז התמונה שונה. למשל, יידרשו logn ספרות בינריות על מנת לייצג מספר שלם הקטן מ- n. אם יאופשר להגדיל את אורך המפתח עם n, כך ש- k=logn, אזי נקבל:
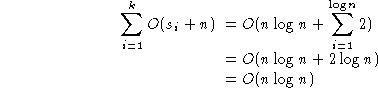
דרך
נוספת להתבונן בכך היא לשים לב לכך שאם טווח המפתח מוגבל ל- (0,bk-1), אז
ניתן להשתמש במיון-בסיס בצורה יעילה אם נאפשר לשכפל
מפתחות כאשר n>bk.
אולם, אם אנו זקוקים למפתחות ייחודיים, k
חייב לגדול לפחות עד ל- logbn.
לכן, כש- n גדל יש צורך ב- logn
שלבים, אשר כך אחד מהם דורש O(n),
ואז מיון-הבסיס הוא כמו מיון-מהיר!
קוד לדוגמא
קוד
זה ממיין מערכים של ערכים שלמים בבסיסים שונים: ניתן לקבוע את מספר הסיביות
("הספרות") לכל בסיס על-ידי קריאה ל- SetRadics.
במחלקת ה- bins נעשה שימוש בכל שלב על מנת לאסוף את הפריטים כאשר
הם ממוינים. ל-ConsBins קוראים על מנת לקבוע סדרת סלים:
כל סל חייב להיות גדול דיו כדי להכיל את כל המערך, כך שמיון-בסיס יכול לעלות
בשימוש רב בזיכרון.
·
Bins.h
·
Bins.c
|
|
|
המשך ל: עצי
חיפוש חזור
ל: תוכן עניינים