6.2 ערמות

מבנה נתונים ואלגוריתמים

 

 

ערמות מבוססות על הרעיון של עץ מלא, שלגביו כבר הובאה הגדרה לא פורמלית.

 

באופן פורמלי:

עץ בינארי נקרא מלא לגמרי (completely full)  אם גובהו h ויש לו 2^h+1-1  צמתים.

עץ הנקרא מושלם (complete) ממולא מצד שמאל ובאופן הבא: כל העלים נמצאים באותה רמה, או בשתי רמות צמודות, וכל הצמתים ברמה הנמוכה ביותר רחוקים ככל הניתן בצדו השמאלי של העץ.

 

עץ בינארי נקרא מושלם אם מתקיימת לפחות אחת מהדרישות הבאות:

·        העץ ריק(!)

·        תת-העץ השמאלי שלו מושלם ובגובה h-1 ותת-העץ הימני שלו מלא לגמרי ובגובה h-2.

·        תת-העץ השמאלי שלו מלא לגמרי ובגובה h-1 ותת-העץ הימני שלו מושלם ובגובה h-1.

 

ערמות

לעץ בינארי יש תכונות של ערמה אם מתקיים אחד מהשניים:

א. העץ ריק.

ב. המפתח שבשורש גדול יותר מהמפתח שבכל בן, ובשני תתי-העצים מתקיימות תכונות הערמה.

 

ערמה יכולה לשמש כתור קדימויות. הפריט בעל הקדימות הגבוהה ביותר יהיה בשורש ומשם יהיה הראשון לצאת. אך לאחר שיוסר השורש יוותרו שני תתי-עצים שמהם יש ליצור ביעילות מחדש עץ אחד בעל תכונות הערמה.

 

הערך של מבנה הערמה הוא בכך שאנו גם יכולים להוציא את הפריט בעל הקדימות הגבוהה ביותר וגם להכניס פריט חדש

בזמן של O(logn).

 

כיצד הדבר מתבצע?

 

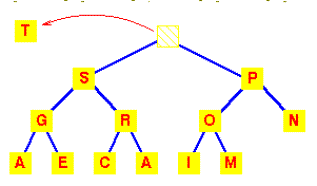נתחיל בערמה זו.                                  

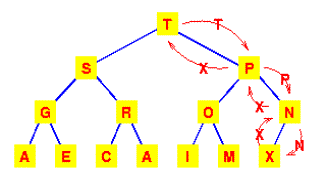
מחיקה תסיר את T מהשורש.

 

 

 

 

 

 

 

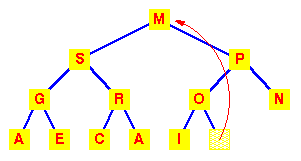על מנת להבין כיצד ניתן לשמר את תכונות

הערמה ניזכר בכלל שלפיו עץ מושלם ממולא

משמאל, כך שהמקום שחייב להתפנות הוא זה

המכיל את M. את M נכניס לשורש הפנוי.

 

 

 

 

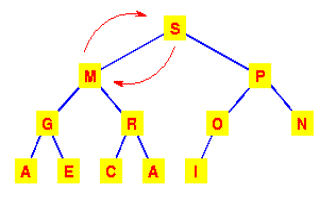
במצב זה מופר התנאי לפיו השורש יהיה גדול

יותר מכל אחד מהילדים, ולכן יש להחליף את

M עם הגדול שבילדיו.  

 

 

 

 

 

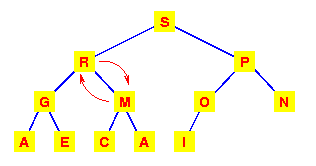
כעת איבד תת-העץ השמאלי עכשיו את תכונות הערימה שלו.

 לכן באותו אופן, גם בו יש להחליף בין M לבנו הגדול ביותר.

 

 

 

 

כעת העץ הינו שוב ערימה, ואנו סיימנו.

 

יש לבצע לכל היותר h החלפות בתת-עץ, של שורש עם אחד מילדיו, כדי להחזיר במלואן את תכונות הערמה. כך שפעולת המחיקה מערמה היא O(h) או O(logn).

 

הוספה לערמה

על מנת להוסיף פריט לערמה, עלינו לבצע הליך הפוך. יש למקם

את הפריטבעמדת העלה הבאה ולהעלות אותו כלפי מעלה. שוב

המדובר ב- O(h) או O(logn) פעולות.

 

 

 

 

אחסון של עצים מושלמים

התכונות של עצים מושלמים יוצרות מנגנון אחסון יעיל ביותר, תוך שימוש ב- n מיקומים רצופים במערך.

 

אם נמספר את הצמתים החל מ- 1 בשורש, ונמקם את השאר באופן הבא:

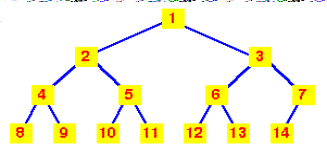
·         הבן השמאלי של צומת k ימוקם כ- k2

·         הבן הימני של צומת k ימוקם כ- k+12

 

אזי אופי ה"מילוי משמאל" של עץ מושלם יבטיח

שהערמה יכולה להיות מאוחסנת במיקומים עוקבים במערך.

 

 

 

 

 

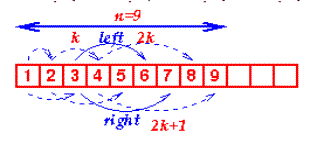
בצורה של מערך ניתן לראות כי הצומת ה- n נמצא תמיד במיקום האינדקס n .

 

 

 

 

הקוד עבור הוצאת הפריט בעל הקדימות הגבוהה ביותר מערמה הוא, באופן טבעי, רקורסיבי. לאחר שמוציאים את פריט השורש (הפריט בעל הקדימות הגבוהה ביותר) ושמים במקומו את הפריט האחרון, פשוט יש לקרוא ל- MoveDown בצורה רקורסיבית עד שמגיעים לתחתית העץ.

 

לחץ כאן להעלות את heap_delete.c

 

שים לב למקרו  LEFT ו -RIGHT שפשוט מציינים את היחסים בין האינדקס של הצמתים של הבנים השמאלי והימני. באופן דומה  מקרו EMPTY מכיל את הקוד לצורך הקביעה האם תת-עץ הוא ריק או לא. הכנסה לתוך הערימה כוללת שיטה דומה, מלבד העובדה כי אנו משתמשים בפונקצית MoveUp על מנת להעביר את האיבר החדשה למיקומו הנכון (עבור פונקצית MoveUp, הוגדר מקרו נוסף אשר מגדיר הורה של איבר שנוסף). ערמות מאפשרות לנו סוג של שיטת מיון הידועה כ- מיון ערימה (heap sort) . אולם נבחן וננתח קודם את שיטות המיון הפשוטות.

 

 

מושגים

 

עץ מושלם

עץ מאוזן שבו המרחק שבין השורש לכל עלה הוא h או h-1.

 

המשך ל: מיון                   חזור ל: תוכן עניינים