13. בעיות NP שלמות

מבנה נתונים ואלגוריתמים

 

 

אם אלגוריתם לפתרון בעיה דורש זמן של O(n^k) עבור איזשהו קבוע k, אזי אנו מסווגים אותו כאלגוריתם פולינומיאלי, ואל הבעיה אנו מתייחסים כבעיה סבירה. אולם לא כל הבעיות ניתנות לפתרון בזמן פולינומיאלי. אם ידוע כי לבעיה אין אלגוריתם הפותר אותה בזמן פולינומיאלי, אזי הבעיה נתפסת כבעיה בלתי-סבירה. אולם, ההבחנה בין שני סיווגים אלו אינה מובנת מאליה. נמחיש זאת בעזרת בחינה של שתי בעיות הנראות דומות: בעיית מסלול אוילר השואלת האם ישנו מסלול בגרף שעובר על כל צלע פעם אחת בלבד, ובעיית מסלול המילטון השואלת האם ישנו מסלול בגרף אשר מבקר בכל קודקוד בדיוק פעם אחת.

 

בעיית מסלול אוילר

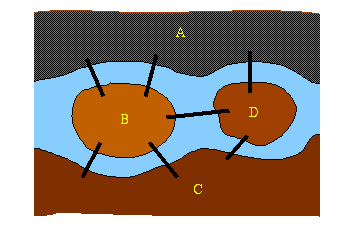
העיר הגרמנית קניגסבורג מהמאה ה- 18 שכנה בסמוך לנהר הפרגל. בתוך הפארק שנבנה על גדות הנהר היו שני איים אשר היו מחוברים על ידי שבעה גשרים. החידה שאלה האם זה אפשרי לסייר בפארק תוך כדי מעבר על כל גשר פעם אחת בלבד.

 

חיפוש ממצה דורש להתחיל בכל נקודה אפשרית ולעבור בכל המסלולים האפשריים מאותה נקודה. חיפוש אחר הפתרון באפן זה הוא בעל סיבוכיות של O(n!). אולם, אוילר הראה כי ניתן לדעת אם קיים מסלול אוילריאני על פי קיום של שני תנאים:

·        ניתן לנוע מכל קודקוד לקודקוד אחר דרך הצלעות (הגרף חייב להיות קשור).

·        לכל קודקוד חייב להיות מספר זוגי של צלעות המחוברות אליו, מלבד לכל היותר שני

חריגים )אלו נקודות ההתחלה והסוף).

 

קל לראות כי אלו תנאים הכרחיים: על מנת להשלים את המעבר יש צורך להיכנס ולצאת מכל נקודה מלבד נקודות ההתחלה והסוף (את ההוכחה הפורמלית שאלו תנאים מספיקים ניתן למצוא בספרות). לכן, אלגוריתם בזמן של O(n) יוכל לקבוע האם קיים מסלול כזה, ומכאן שבעיית מסלול אוילר ניתנת לפתרון בזמן פולינומיאלי .

 

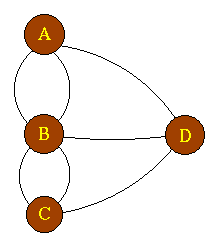
נתרגם את המפה לגרף בו כל צומת מייצג אדמה וכל קשת מייצגת גשר.

ניתן לראות בקלות כי לבעיית הגשרים של קניגסבורג אין פתרון. עם זאת ניתן לראות כי קיים מסלול המילטוני.

אם זאת לא קיים אלגוריתם יעיל לבדיקה האם קיים מסלול המילטוני

 

בעיית מסלול המילטון

מבט נוסף במפת המייצגת את מערכת הגשרים בעיר קינגסבורג מראה כי מסלול המילטוני אכן קיים בה. אולם, לא ידוע על אלגוריתם יעיל לקביעה האם קיים מסלול המילטוני בגרף נתון! לכן, בעיית מסלול המילטון אינה נכללת בקבוצת הבעיות הפתירות בזמן פולינומיאלי, המכונה גם בשם

מחלקת P. עם זאת, בעיית מסלול המילטון נכללת בקבוצה אחרת של בעיות הנקראת מחלקת NP. קבוצה הבעיות הנכללות במחלקה זו מתאפיינת בכך שניתן לאשר נכונות של פתרון המוצע להן בזמן פולינומיאלי. די באלגוריתם הדורש O(n²) זמן בכדי לאשר כי מסלול נתון הוא המילטוני.

 

עדיין לא ידוע האם P = NP, אולם רוב החוקרים מאמינים כי P ו- NP הן מחלקות שונות. בכל אופן מה שברור הוא כי P Í NP, כלומר, לגבי כל הבעיות הניתנות לפתרון בזמן פולינומיאלי, ניתן גם לאשר נכונות פתרון בזמן פולינומיאלי.   

 

ידועות בעיות רבות הנמצאות ב- NP. להלן מספר דוגמאות:

 

מספרים מורכבים

הקביעה האם מספר יכול להיכתב כתוצר של שני מספרים אחרים ידועה כבעיית המספרים המורכבים. אם פתרון נמצא - קל לאשרו, אך אין דרך יעילה לדעת האם קיים פתרון.

 

התאמת שותפים

זוהי בעיה של הצבה יחד של שותפים מתאימים לדירה. נניח כי יש מספר כלשהו של סטודנטים אותם יש לפזר בחדרי המעונות. הסטודנטים יכולים להיות מיוצגים על ידי קדקודים בגרף בעל צלעות המקשרות זוגות סטודנטים המתאימים לדיור משותף. לצורך הצבת שני סטודנטים בכל חדר קיים אלגוריתם ממחלקה P, אך אם יש להציב שלושה סטודנטים בכל חדר הבעיה היא ממחלקת NP.

 

ניתנות לסיפוק של ביטויים בוליאנים (boolean satisfiabiliti)

נניח כי נתון ביטוי בוליאני שרירותי בעל n משתנים:

a ₁ op a ₂ op .. op a _n 

כאשר כל op הוא אופרטור בוליאני כמו: וגם, או וכו'.

 

האם ניתן למצוא הצבה של אמת/שקר ל-  a _i כך שהביטוי יהיה אמת? בעיה זו שקולה לבעיית

ספיקות המעגלים השואלת האם ניתן למוצא קלט שיוצר ערך אמת בפלט של מעגל המורכב משערים לוגים שרירותיים.

 

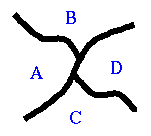
צביעת מפה

בעיית צביעת מפה בשלושה צבעים שואלת האם ניתן לצבוע מפה כך שאין שתי ארצות סמוכות הצבועות באותו צבע. בעת כל ניחוש של פתרון, מיד ניתן להיווכח האם הוא עומד בתנאים.

בעיה זו נפתרת בקלות אם ישנם רק שני צבעים - אז חובה שלא תהיה אף נקודה שבה נפגשות מספר אי-זוגי של ארצות. גם כאשר המפה נצבעת בארבעה צבעים הפתרון מהיר - קיימת הוכחה שארבעה צבעים מספיקים לצביעת כל מפה, תחת התנאי האמור. 

 

הבעיה ניתנת לייצוג על ידי גרף: כל קודקוד מייצג מדינה וצלע מצויירת בין שני קדקודים אם הם חולקים גבול משותף.

 

לפתרון הבעיה יש יישום כללי יותר. אם אנו מתכננים לוח זמנים לעבודה במפעל, כל קודקוד מייצג משימה האמורה להתבצע , והקדקודים מקושרים ביניהם על ידי צלע אם הם חולקים משאב משותף, כמו שימוש במכונה מסוימת. צביעה של הקדקודים בשלושה צבעים מאפשרת תכנון לוח זמני עבודה של 3 משמרות במפעל.

 

רדוקציות

נאמר שבעיה Q ניתנת לרדוקציה לבעיה אחרת Q' אם ניתן לנסח מחדש כל מופע של Q כמופע של Q', שפתרונו מספק פתרון למופע של Q. אם בעיה Q ניתנת לרדוקציה לבעיה אחרת Q', אז במובן מסוים Q אינה קשה יותר לפתרון מאשר Q.

 

אם ניתן לעבור מבעיה L ₁  לבעיה L ₂ בזמן פולינומיאלי, נאמר שהרדוקציה היא פולינומיאלית ונסמן L ₁ ≤ _p L ₂ . הרדוקציה הפולינומיאלית מסייעת להגדרת מחלקה נוספת של בעיות - בעיות NP שלמות (NP-complete).                  

 

 

בעיות NP שלמות

קבוצת הבעיות הנקראות NP שלמות מהווה תת-מחלקה מיוחדת של כל קבוצת הבעיות ב- NP. נגדיר בעיה L כ- NP שלמה אם:

1. L Î NP, וגם

2. L'  ≤ _p L לכל L' Î NP.

אם בעיה מקיימת את תכונה השניה, אולם אינה מקיימת בהכרח את הראשונה, נאמר כי זו בעיה NP קשה (NP-hard).  

 

ברגע שנדע כי בעיה מסוימת היא NP שלמה, נוכל להשתמש ברדוקציה פולינומיאלית כדי להוכיח כי גם בעיות אחרות הן NP שלמות. ואכן ב- 1971 הוכח כי בעיית הניתנות לסיפוק של ביטויים בוליאנים (boolean satisfiabiliti), השקולה לבעיית ספיקות המעגלים (שתי הבעיות תוארו בקצרה לעיל), היא NP שלמה. הוכחה זו אפשרה להוכיח כי בעיות אחרות שייכות גם הן למחלקת בעיות NP השלמות, וככל שהולכת ומתארכת רשימת הבעיות המוכחות כ- NP שלמות, קל יותר להוכיח את שלמותן של בעיות נוספות ב- NP. 

 

 

מושגים

 

מסלול אוילר

            מסלול בגרף העובר על כל צלע פעם אחת בלבד.

מסלול המילטוני

            מסלול העובר דרך כל קודקוד בגרף בדיוק פעם אחת.

מחלקת P

            קבוצת הבעיות הפתירות בזמן פולינומיאלי.

מחלקת NP  

קבוצה הבעיות שניתן לאשר נכונות של פתרון המוצע עבורן בזמן פולינומיאלי.

בעיות NP שלמות

            תת-מחלקה מיוחדת של כל קבוצת הבעיות ב- NP. בעיה L תוגדר כ- NP שלמה אם

  1. L Î NP, וגם

   2. L'  ≤ _p L לכל L' Î NP.

 

המשך ל: משחקים              חזור ל: תוכן עניינים