עץ אדום שחור - הוספת איברלצורך פעולת ההוספה נעזרים בפעולות סיבוב
לימין או לשמאל. פעולות אלה משנות את מבנה העץ אך שומרות על
תכונת היותו עץ חיפוש בינארי. תהליך ההוספה:1. מוסיפים צומת כמו בעץ חיפוש בינארי
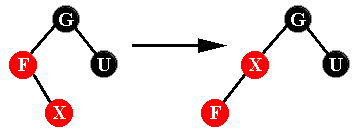
רגיל. א. F הוא שורש העץ: נצבע את F בשחור. כעת העץ חוקי. ב. U אדום: נצבע את F ו-U בשחור ואת G באדום. כעת נחזור לשלב 3 אך נתייחס ל-G כאל הצומת החדש. ג. X בן ימני של F וגם U בן ימני של G (או ששניהם בנים שמאליים): נבצע סיבוב לשמאל של תת העץ ששורשו F (או סיבוב ימני במקרה שהם היו בנים ימניים) ונעבור למקרה ד'.
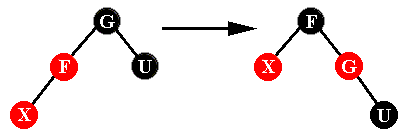
ד. X בן שמאלי של F ו-U בן ימני של G (או להיפך): נבצע סיבוב לימין של העץ ששורשו G. (או סיבוב לשמאל במקרה ההפוך). נצבע את G באדום ו-F בשחור. כעת העץ חוקי.
RedBlackInsert (T,x)
{
TreeInsert (T,x)
color (x) <- Red
while x != root (T) and color (p(x))==Red
if p(x)==left(p(p(x)))
y <- right(p(p(x)))
if color(y)==Red
color(p(x)) <- Black
color(y) <- Black
color(p(p(x))) <- Red
x <- p(p(x))
else
if x==right(p(x))
x <- p(x)
RotateLeft(T,x)
color(p(x)) <- Black
color(p(p(x))) <- Red
RotateRight(T, p(p(x)))
else
/* this is the same as the "then" clause,
* with "right" and "left" interchanged */
color(root(T)) <- Black
}
|
|