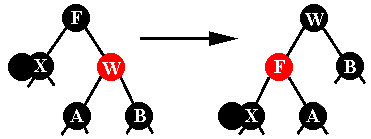
עץ אדום שחור - מחיקת איברלצורך פעולת המחיקה נעזרים בפעולות סיבוב לימין או לשמאל. פעולות אלה משנות את מבנה העץ אך שומרות על תכונת היותו עץ חיפוש בינארי. בעת ביצוע המחיקה, נתייחס ל-NIL כאל עלה שחור (כלומר אם לצומת אין בן, נסמן כאילו יש לו בן שחור). תהליך המחיקה:נסמן: Y = הצומת אותו אנחנו מוחקים. אם ל-Y יש שני בנים: נשים במקום Y את האיבר בעל הערך המינימלי בתת העץ הימני ואז נמחק את האיבר המינימלי באותה שיטה. בסופו של דבר נגיע למצב שבו ל-Y יש בן אחד או אין בנים. 1. אם Y אדום: תכונות העץ נשמרות. א. W אדום: נסובב את העץ ששורשו F לכיוון ההפוך מ- W. נצבע את W
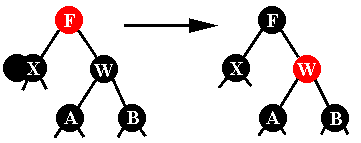
בשחור, F באדום ונמשיך לפי אחד המקרים הבאים. ב. W שחור, F אדום, שני בניו של W שחורים: נצבע את F בשחור, W באדום
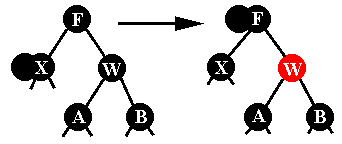
ויתקבל עץ חוקי. ג. W שחור, F שחור, בניו של W שחורים: נצבע את W באדום ונסמן את
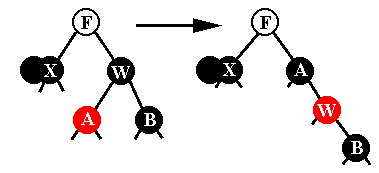
F כמכיל שני שחורים (במקום X) ואז נמשיך לפי אחד המקרים. ד. W שחור, ל-W יש בן אדום (שנסמן אותו A) נבדוק את צבע בניו של W: ד1. אם W בן ימני של F וגם יש לו בן שחור ימני: נסובב את W לימין,
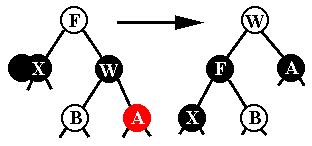
נצבע את A בשחור, W באדום, ונעבור למקרה ד3. ד2. אם W בן שמאלי של F וגם יש לו בן שחור שמאלי: נסובב את W לשמאל ונפעל כמו במקרה ד1. ד3. במקרים האחרים: נסובב את F לכיוון X, נצבע את F בשחור, W בצבע
שהיה ל-F קודם, ו-A בשחור ונקבל עץ חוקי.
RedBlackDelete(T,z)
{
if left(z)==nil(T) or right(z)==nil(T)
y <-- z
else
y <-- TreeSuccessor(z)
if left(y) != nil(T)
x <-- left(y)
else
x <-- right(y)
p(x) <-- p(y)
if p(y) == nil(T)
root(T) <-- x
else
if y==left(p(y))
left(p(x)) <-- x
else
right(p(y)) <-- x
if y != z
key(z) <-- key(y)
/* if y has other fields, copy them too */
if color(y)==Black
then RBDeleteFixup(T,x)
}
RBDeleteFixup(T,x)
{
while x != root(T) and color(x)==Black
if x==left(p(x))
w <-- right(p(x))
if color(w) == Red
color(w) <-- Black
color(p(x)) <-- Red
RotateLeft(T,p(x))
w <-- right(p(x))
if color(left(w))==Black and color(right(w))==Black
color(w) <-- Red
x <-- parent(x)
else
if color(right(w)) == Black
color(left(w)) <-- Black
color(w) <-- Red
RotateRight(T,w)
w <-- right(p(x))
color(w) <-- color(p(x))
color(p(x)) <-- Black
color (right(w)) <-- Black
RotateLeft(T,p(x))
x <-- root(T)
else
/* this is same as "then" clause,
* except that right and left are exchanged */
color(x) <--Black
}
|
|