|
השלב הסופי
Add Round Key (הוספת מפתח מחזור). זה פשוט לעשות
XOR של התוצאה הקודמת עם תת המפתח של מחזור
הנוכחי.
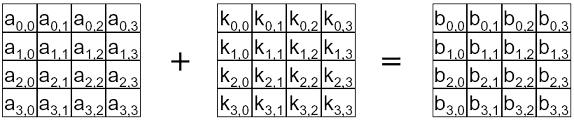
למרות שבתחילת העמוד כבר
הצגנו דיאגראמה צבעונית תלת ממדית אפשר גם להציג את המחזור של
Rijndael בצורה יותר שגרתית:
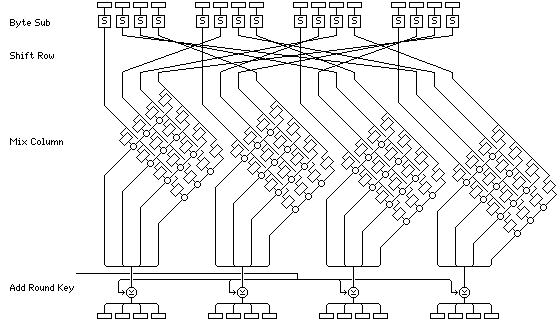
המחזור הסופי הנוסף משמיט
את שלב ה-Mix Column, אבל
חוץ מזה זה מחזור רגיל.
לכן, הרצף של השלבים ב-Rijndael הוא:
ARK
BSB
SR
MC
ARK
BSB
SR
MC
ARK
...
BSB
SR
MC
ARK
BSB
SR
ARK
בגלל שזה מתחיל ומסתיים עם
השלב Add Round Key,
אין שלב מבוזבז בהתחלה או בסוף. רצף ההשתלשלות חשוב גם להקלה על הפענוח.
למרות שהרצף אינו
סימטרי אפשר לשנות חלק מהשלבים ב-Rijndael
בלי להשפיע על ההצפנה. את שלב ה-Byte Sub אפשר לעשות
באותה המידה לפני Shift Row כמו
שאחריו.
זה ישנה את
A BSMA BSMA ... BSMA BSA
ל
A SBMA SBMA ... SBMA SBA
אם, מצד שני, שמרנו על הרצף
המקומי, אנו נקבל
ASB AMSB ... AMSB AMSB A
למרות שהם נראים דומים, חוץ
מהמיקום של הרווחים שרק מסמן את מה שאנו קראנו לזה מחזורים באלגוריתמים, כאשר רצף "MA"
מופיע באלגוריתם שעבר שינוי, אך שקול, הרצף "AM"
מופיעה ברצף הפוך, הדרוש לפענוח.
כמובן השלבים שבהם צריך
להפוך הם: ARK הוא
XOR, זאת אומרת הוא ההפיך של עצמו, אבל
מטריצה בשלב ה - Mix Column צריכה להתחלף עם המטריצה
ההפוכה, וה-S-box בשלב
ה-Byte Sub צריך להתחלף עם ההפיך שלו בשלב הפענוח.
אבל מה לגבי החלפה בין
MA ובין AM? האם אנו צריכים לשנות את סדר הפעולות וסדר הפענוח?
לא; עם הכפלת מטריצה,
התכונה הדסטריביוטיבית גם כן חלה, ז"א מפתחות מחזור המשתתפים בהפיכה הזאת
פשוט צריכים להיות מוכפלים ע"י מטריצה Mix Column
(הפוכה), ואז אפשר לעשות איתם XOR
באותו הזמן (כמובן בסדר הפוך) כמו שעשינו בהצפנה. (XOR
מתאים להוספה בשדה גלואה ( 28 ), שבו
המכפלות מבוצעות).
המטריצה לשלב ה -
Mix Column ההפוכה היא:
|
14 11 13 9
9 14 11 13
13 9 14 11
11 13 9 14 |
כמו שאפשר לבדוק בקלות, ע"י
שימוש בסימטריה, וכאשר התשובה ידועה:
1110 1011 1101 1001 01 00 00 00
1001 1110 1011 1101 00 01 00 00
1101 1001 1110 1011 00 00 01 00
1011 1101 1001 1110 00 00 00 01
111 101 110 100 01
01 00 00
110 100 111 101 00
00 01 01
1100 1000 1110 1010 00 00 10 10
1011 1101 1000 1110 01 01 10 10
0 0
1 0 01 01 10 11
מכיוון שעכשיו אנו מבצעים
הכפלה בשדה גלואה במספרים גדולים יותר, דוגמא אחרת של הכפלה בשדה גלואה יכולה להיות
שימושית. כדי להחליף מחרוזת בינארית 10100011 ב-14 ב-GF
נעבוד כך:
10100011
1110 *
------------
10100011
10100011
10100011
------------
11011010010
100011011
------------
1010111110
100011011
------------
10001000
הדוגמא הזאת מדגימה איך שוב
ושוב מתבצע XOR לערך 10001011, מוזז
שמאלה בכמות הפעמים הנדרשת, כדי למחוק סיבית ראשונה של התוצאה על מנת לקבל תוצאה
סופית שנכנסת ל-8 סיביות.
|

