This is a Chapter from the Handbook of Applied Cryptography, by A

This is a Chapter from the Handbook of Applied Cryptography, by A. Menezes, P. van

Oorschot, and S. Vanstone, CRC Press, 1996.

For further information, see www.cacr.math.uwaterloo.ca/hac

CRC Press has granted the following speci_c permissions for the electronic version of this

book:

Permission is granted to retrieve, print and store a single copy of this chapter for

personal use. This permission does not extend to binding multiple chapters of

the book, photocopying or producing copies for other than personal use of the

person creating the copy, or making electronic copies available for retrieval by

others without prior permission in writing from CRC Press.

Except where over-ridden by the speci_c permission above, the standard copyright notice

from CRC Press applies to this electronic version:

Neither this book nor any part may be reproduced or transmitted in any form or

by any means, electronic or mechanical, including photocopying, micro_lming,

and recording, or by any information storage or retrieval system, without prior

permission in writing from the publisher.

The consent of CRC Press does not extend to copying for general distribution,

for promotion, for creating new works, or for resale. Speci_c permission must be

obtained in writing from CRC Press for such copying.

c 1997 by CRC Press, Inc.

x1.11

One approach to distributing public-keys is the so-called Merkle channel (see Simmons

[1144, p.387]). Merkle proposed that public keys be distributed over so many independent

public channels (newspaper, radio, television, etc.) that it would be improbable for an adversary

to compromise all of them.

In 1979 Kohnfelder [702] suggested the idea of using public-key certificates to facilitate

the distribution of public keys over unsecured channels, such that their authenticity can be

verified. Essentially the same idea, but by on-line requests, was proposed by Needham and

Schroeder (ses Wilkes [1244]).

Aprovably secure key agreement protocol has been proposedwhose security is based on the

Heisenberg uncertainty principle of quantum physics. The security of so-called quantum

cryptography does not rely upon any complexity-theoretic assumptions. For further details

on quantum cryptography, consult Chapter 6 of Brassard [192], and Bennett, Brassard, and

Ekert [115].

x1.12

For an introduction and detailed treatment of many pseudorandom sequence generators, see

Knuth [692]. Knuth cites an example of a complex scheme to generate random numbers

which on closer analysis is shown to produce numberswhich are far from random, and concludes:

...random numbers should not be generated with a method chosen at random.

x1.13

The seminal work of Shannon [1121] on secure communications, published in 1949, remains

as one of the best introductions to both practice and theory, clearly presenting many

of the fundamental ideas including redundancy, entropy, and unicity distance. Various models

under which security may be examined are considered by Rueppel [1081], Simmons

[1144], and Preneel [1003], among others; see also Goldwasser [476].

17. A function or mapping f : A -! B is a rule which assigns to each element a in A

precisely one element b in B. If a 2 A is mapped to b 2 B then b is called the image

of a, a is called a preimage of b, and this is written f(a) = b. The set A is called the

domain of f, and the set B is called the codomain of f.

18. A function f : A -! B is 1-1 (one-to-one) or injective if each element in B is the

image of at most one element in A. Hence f(a1) = f(a2) implies a1 = a2.

19. A function f : A -! B is onto or surjective if each b 2 B is the image of at least

one a 2 A.

20. A function f : A -! B is a bijection if it is both one-to-one and onto. If f is a

bijection between finite sets A and B, then jAj = jBj. If f is a bijection between a

set A and itself, then f is called a permutation on A.

21. ln x is the natural logarithm of x; that is, the logarithm of x to the base e.

22. lg x is the logarithm of x to the base 2.

23. exp(x) is the exponential function ex.

24. Pn

i=1 ai denotes the sum a1 + a2 + _ _ _ + an.

25. Qn

i=1 ai denotes the product a1 _ a2 _ _ _ _ _ an.

26. For a positive integer n, the factorial function is n! = n(n - 1)(n - 2) _ _ _ 1. By

convention, 0! = 1.

Mathematical Background

Contents in Brief

2.1 Probability theory : : : : : : : : : : : : : : : : : : : : : : : : : : 50

2.2 Information theory : : : : : : : : : : : : : : : : : : : : : : : : : 56

2.3 Complexity theory : : : : : : : : : : : : : : : : : : : : : : : : : 57

2.4 Number theory : : : : : : : : : : : : : : : : : : : : : : : : : : : 63

2.5 Abstract algebra : : : : : : : : : : : : : : : : : : : : : : : : : : 75

2.6 Finite fields : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 80

2.7 Notes and further references : : : : : : : : : : : : : : : : : : : : 85

This chapter is a collection of basic material on probability theory, information theory,

complexity theory, number theory, abstract algebra, and finite fields that will be used

throughout this book. Further background and proofs of the facts presented here can be

found in the references given in x2.7. The following standard notation will be used throughout:

1. Z denotes the set of integers; that is, the set f: : : ;-2;-1; 0; 1; 2; : : :g.

2. Q denotes the set of rational numbers; that is, the set fa

b j a; b 2 Z; b 6= 0g.

3. R denotes the set of real numbers.

4. _ is the mathematical constant; _ _ 3:14159.

5. e is the base of the natural logarithm; e _ 2:71828.

6. [a; b] denotes the integers x satisfying a _ x _ b.

7. bxc is the largest integer less than or equal to x. For example, b5:2c = 5 and

b-5:2c = -6.

8. dxe is the smallest integer greater than or equal to x. For example, d5:2e = 6 and

d-5:2e = -5.

9. IfAis a finite set, then jAj denotes the number of elements inA, called the cardinality

of A.

10. a 2 A means that element a is a member of the set A.

11. A _ B means that A is a subset of B.

12. A _ B means that A is a proper subset of B; that is A _ B and A 6= B.

13. The intersection of sets A and B is the set A \ B = fx j x 2 A and x 2 Bg.

14. The union of sets A and B is the set A [ B = fx j x 2 A or x 2 Bg.

15. The difference of sets A and B is the set A - B = fx j x 2 A and x 62 Bg.

16. The Cartesian product of sets A and B is the set A _ B = f(a; b) j a 2 A and b 2

Bg. For example, fa1; a2g _ fb1; b2; b3g = f(a1; b1); (a1; b2); (a1; b3); (a2; b1),

2.1 Probability theory

2.1.1 Basic definitions

2.1 Definition An experiment is a procedure that yields one of a given set of outcomes. The

individual possible outcomes are called simple events. The set of all possible outcomes is

called the sample space.

This chapter only considers discrete sample spaces; that is, sample spaces with only

finitely many possible outcomes. Let the simple events of a sample space S be labeled

s1; s2; : : : ; sn.

2.2 Definition A probability distribution P on S is a sequence of numbers p1; p2; : : : ; pn that

are all non-negative and sumto 1. The number pi is interpreted as the probability of si being

the outcome of the experiment.

2.3 Definition An event E is a subset of the sample space S. The probability that event E

occurs, denoted P(E), is the sumof the probabilities pi of all simple events si which belong

to E. If si 2 S, P(fsig) is simply denoted by P(si).

2.4 Definition If E is an event, the complementary event is the set of simple events not belonging

to E, denoted E.

2.5 Fact Let E _ S be an event.

(i) 0 _ P(E) _ 1. Furthermore, P(S) = 1 and P(;) = 0. (; is the empty set.)

(ii) P(E) = 1 - P(E).

(iii) If the outcomes in S are equally likely, then P(E) = jEj

jSj .

2.6 Definition Two events E1 and E2 are called mutually exclusive if P(E1 \E2) = 0. That

is, the occurrence of one of the two events excludes the possibility that the other occurs.

2.7 Fact Let E1 and E2 be two events.

(i) If E1 _ E2, then P(E1) _ P(E2).

(ii) P(E1 [ E2) + P(E1 \ E2) = P(E1) + P(E2). Hence, if E1 and E2 are mutually

exclusive, then P(E1 [ E2) = P(E1) + P(E2).

2.1.2 Conditional probability

2.8 Definition Let E1 and E2 be two events with P(E2) > 0. The conditional probability of

E1 given E2, denoted P(E1jE2), is

P(E1jE2) =

P(E1 \ E2)

P(E2)

P(E1jE2) measures the probability of event E1 occurring, given that E2 has occurred.

2.9 Definition Events E1 and E2 are said to be independent if P(E1 \E2) = P(E1)P(E2).

Observe that ifE1 andE2 are independent, thenP(E1jE2) = P(E1) andP(E2jE1) =

P(E2). That is, the occurrence of one event does not influence the likelihood of occurrence

of the other.

2.10 Fact (Bayes’ theorem) If E1 and E2 are events with P(E2) > 0, then

P(E1jE2) =

P(E1)P(E2jE1)

P(E2)

2.1.3 Random variables

Let S be a sample space with probability distribution P.

2.11 Definition A random variable X is a function from the sample space S to the set of real

numbers; to each simple event si 2 S, X assigns a real number X(si).

Since S is assumed to be finite, X can only take on a finite number of values.

2.12 Definition LetX be a random variable on S. Theexpected value or mean ofX isE(X) = Psi2S X(si)P(si).

2.13 Fact Let X be a random variable on S. Then E(X) = Px2R x _ P(X = x).

2.14 Fact IfX1;X2; : : : ;Xm are random variables on S, and a1; a2; : : : ; am are real numbers,

then E(Pm

i=1 aiXi) = Pm

i=1 aiE(Xi).

2.15 Definition The variance of a random variableX of mean _ is a non-negative number de-

fined by

Var(X) = E((X - _)2):

The standard deviation of X is the non-negative square root of Var(X).

If a random variable has small variance then large deviations from the mean are unlikely

to be observed. This statement is made more precise below.

2.16 Fact (Chebyshev’s inequality) Let X be a random variable with mean _ = E(X) and

variance _2 = Var(X). Then for any t > 0,

P(jX - _j _ t) _

2.1.4 Binomial distribution

2.17 Definition Let n and k be non-negative integers. The binomial coefficient _n

k_is the number

of different ways of choosing k distinct objects from a set of n distinct objects, where

the order of choice is not important.

2.18 Fact (properties of binomial coefficients) Let n and k be non-negative integers.

(i) _n

k_ = n!

k!(n-k)! .

(ii) _n

k_ = _ n

n-k_.

(iii) _n+1

k+1_ = _n

k_+ _ n

k+1_.

2.19 Fact (binomial theorem) For any real numbers a, b, and non-negative integer n, (a+b)n = Pn

k=0 _n

k_akbn-k.

2.20 Definition A Bernoulli trial is an experiment with exactly two possible outcomes, called

success and failure.

2.21 Fact Suppose that the probability of success on a particular Bernoulli trial is p. Then the

probability of exactly k successes in a sequence of n such independent trials is

k_pk(1 - p)n-k; for each 0 _ k _ n: (2.1)

2.22 Definition The probability distribution (2.1) is called the binomial distribution.

2.23 Fact The expected number of successes in a sequence of n independent Bernoulli trials,

with probability p of success in each trial, is np. The variance of the number of successes

is np(1 - p).

2.24 Fact (law of large numbers) Let X be the random variable denoting the fraction of successes

in n independent Bernoulli trials, with probability p of success in each trial. Then

for any _ > 0,

P(jX - pj > _) -! 0; as n -! 1:

In other words, as n gets larger, the proportion of successes should be close to p, the

probability of success in each trial.

2.1.5 Birthday problems

2.25 Definition

(i) For positive integers m, n with m _ n, the number m(n) is defined as follows:

m(n) = m(m- 1)(m - 2) _ _ _ (m - n + 1):

(ii) Let m; n be non-negative integers with m _ n. The Stirling number of the second

kind, denoted _m

n , is

n_ =

n Xk=0

(-1)n-k_n

k_km;

with the exception that _0

0 = 1.

The symbol _m

n counts the number of ways of partitioning a set of m objects into n

non-empty subsets.

2.26 Fact (classical occupancy problem) An urn hasmballs numbered 1 to m. Suppose that n

balls are drawn from the urn one at a time, with replacement, and their numbers are listed.

The probability that exactly t different balls have been drawn is

P1(m; n; t) = _n

t_m(t)

mn ; 1 _ t _ n:

The birthday problem is a special case of the classical occupancy problem.

2.27 Fact (birthday problem) An urn has m balls numbered 1 to m. Suppose that n balls are

drawn from the urn one at a time, with replacement, and their numbers are listed.

(i) The probability of at least one coincidence (i.e., a ball drawn at least twice) is

P2(m; n) = 1 - P1(m; n; n) = 1 -

m(n)

mn ; 1 _ n _ m: (2.2)

If n = O(

m) (see Definition 2.55) and m -! 1, then

P2(m; n) -! 1 - exp_-

n(n - 1)

+ O_ 1

m__ _ 1 - exp_-

2m_:

(ii) As m -! 1, the expected number of draws before a coincidence isp_m

2 .

The following explains why probability distribution (2.2) is referred to as the birthday

surprise or birthday paradox. The probability that at least 2 people in a room of 23 people

have the same birthday is P2(365; 23) _ 0:507, which is surprisingly large. The quantity

P2(365; n) also increases rapidly as n increases; for example, P2(365; 30) _ 0:706.

A different kind of problem is considered in Facts 2.28, 2.29, and 2.30 below. Suppose

that there are two urns, one containing m white balls numbered 1 to m, and the other containingmred

balls numbered 1 tom. First, n1 balls are selected from the first urn and their

numbers listed. Then n2 balls are selected from the second urn and their numbers listed.

Finally, the number of coincidences between the two lists is counted.

2.28 Fact (model A) If the balls from both urns are drawn one at a time, with replacement, then

the probability of at least one coincidence is

P3(m; n1; n2) = 1 -

mn1+n2 Xt1;t2

m(t1+t2)_n1

t1__n2

t2_;

where the summation is over all 0 _ t1 _ n1, 0 _ t2 _ n2. If n = n1 = n2, n = O(

and m -! 1, then

P3(m; n1; n2) -! 1 - exp_-

m _1 + O_ 1

m___ _ 1 - exp_-

m_:

2.29 Fact (model B) If the balls from both urns are drawn without replacement, then the probability

of at least one coincidence is

P4(m; n1; n2) = 1 -

m(n1+n2)

m(n1)m(n2)

If n1 = O(

m), n2 = O(

m), and m -! 1, then

P4(m; n1; n2) -! 1 - exp_-

n1n2

m _1 +

n1 + n2 - 1

+ O_ 1

m___:

2.30 Fact (model C) If the n1 white balls are drawn one at a time, with replacement, and the n2

red balls are drawn without replacement, then the probability of at least one coincidence is

P5(m; n1; n2) = 1 - _1 -

m_n1

If n1 = O(

m), n2 = O(

m), and m -! 1, then

P5(m; n1; n2) -! 1 - exp_-

n1n2

m _1 + O _ 1

m___ _ 1 - exp _-

n1n2

m _:

2.1.6 Random mappings

2.31 Definition Let Fn denote the collection of all functions (mappings) from a finite domain

of size n to a finite codomain of size n.

Models where random elements of Fn are considered are called random mappings

models. In this section the only random mappings model considered iswhere every function

from Fn is equally likely to be chosen; such models arise frequently in cryptography and

algorithmic number theory. Note that jFnj = nn, whence the probability that a particular

function from Fn is chosen is 1=nn.

2.32 Definition Let f be a function in Fn with domain and codomain equal to f1; 2; : : : ; ng.

The functional graph of f is a directed graph whose points (or vertices) are the elements

f1; 2; : : : ; ng and whose edges are the ordered pairs (x; f(x)) for all x 2 f1; 2; : : : ; ng.

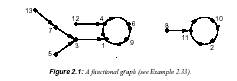
2.33 Example (functional graph)Consider the function f : f1; 2; : : : ; 13g -!f1; 2; : : : ; 13g

defined by f(1) = 4, f(2) = 11, f(3) = 1, f(4) = 6, f(5) = 3, f(6) = 9, f(7) = 3,

f(8) = 11, f(9) = 1, f(10) = 2, f(11) = 10, f(12) = 4, f(13) = 7. The functional

graph of f is shown in Figure 2.1. _

As Figure 2.1 illustrates, a functional graph may have several components (maximal

connected subgraphs), each component consisting of a directed cycle and some directed

trees attached to the cycle.

2.34 Fact As n tends to infinity, the following statements regarding the functional digraph of a

random function f from Fn are true:

(i) The expected number of components is 1

(ii) The expected number of points which are on the cycles is p_n=2.

(iii) The expected number of terminal points (points which have no preimages) is n=e.

(iv) The expected number of k-th iterate image points (x is a k-th iterate image point if

x = f(f(_ _ _ f

| {z } k times

(y) _ _ _ )) for some y) is (1-_k)n, where the _k satisfy the recurrence

_0 = 0, _k+1 = e-1+_k for k _ 0.

2.35 Definition Let f be a random function from f1; 2; : : : ; ng to f1; 2; : : : ; ng and let u 2

f1; 2; : : : ; ng. Consider the sequence of points u0; u1; u2; : : : defined by u0 = u, ui =

f(ui-1) for i _ 1. In terms of the functional graph of f, this sequence describes a path that

connects to a cycle.

(i) The number of edges in the path is called the tail length of u, denoted _(u).

(ii) The number of edges in the cycle is called the cycle length of u, denoted _(u).

(iii) The rho-length of u is the quantity _(u) = _(u) + _(u).

(iv) The tree size of u is the number of edges in the maximal tree rooted on a cycle in the

component that contains u.

(v) The component size of u is the number of edges in the component that contains u.

(vi) The predecessors size of u is the number of iterated preimages of u.

2.36 Example The functional graph in Figure 2.1 has 2 components and 4 terminal points. The

point u = 3 has parameters _(u) = 1, _(u) = 4, _(u) = 5. The tree, component, and

predecessors sizes of u = 3 are 4, 9, and 3, respectively. _

2.37 Fact As n tends to infinity, the following are the expectations of some parameters associated

with a random point in f1; 2; : : : ; ng and a random function from Fn: (i) tail length: p_n=8 (ii) cycle length: p_n=8 (iii) rho-length: p_n=2 (iv) tree size: n=3 (v) component

size: 2n=3 (vi) predecessors size: p_n=8.

2.38 Fact As n tends to infinity, the expectations of the maximumtail, cycle, and rho lengths in

a random function from Fn are c1

n, c2

n, and c3

n, respectively, where c1 _ 0:78248,

c2 _ 1:73746, and c3 _ 2:4149.

Facts 2.37 and 2.38 indicate that in the functional graph of a random function, most

points are grouped together in one giant component, and there is a small number of large

trees. Also, almost unavoidably, a cycle of length about

n arises after following a path of

length

n edges.

2.2 Information theory

2.2.1 Entropy

LetX be a random variable which takes on a finite set of values x1; x2; : : : ; xn, with probability

P(X = xi) = pi, where 0 _ pi _ 1 for each i, 1 _ i _ n, and wherePn

i=1 pi = 1.

Also, let Y and Z be random variables which take on finite sets of values.

The entropy ofX is a mathematical measure of the amount of information provided by

an observation ofX. Equivalently, it is the uncertainity about the outcome before an observation

of X. Entropy is also useful for approximating the average number of bits required

to encode the elements of X.

2.39 Definition The entropy or uncertainty of X is defined to be H(X) = -Pn

i=1 pi lg pi =

i=1 pi lg _ 1

pi _where, by convention, pi _ lg pi = pi _ lg _ 1

pi _ = 0 if pi = 0.

2.40 Fact (properties of entropy) Let X be a random variable which takes on n values.

(i) 0 _ H(X) _ lg n.

(ii) H(X) = 0 if and only if pi = 1 for some i, and pj = 0 for all j 6= i (that is, there is

no uncertainty of the outcome).

(iii) H(X) = lgn if and only if pi = 1=n for each i, 1 _ i _ n (that is, all outcomes are

equally likely).

2.41 Definition The joint entropy of X and Y is defined to be

H(X; Y) = -Xx;y

P(X = x; Y = y) lg(P(X = x; Y = y));

where the summation indices x and y range over all values of X and Y , respectively. The

definition can be extended to any number of random variables.

2.42 Fact If X and Y are random variables, then H(X; Y ) _ H(X)+H(Y ), with equality if

and only if X and Y are independent.

2.43 Definition If X, Y are random variables, the conditional entropy of X given Y = y is

H(XjY = y) = -Xx

P(X = xjY = y) lg(P(X = xjY = y));

where the summation index x ranges over all values of X. The conditional entropy of X

given Y , also called the equivocation of Y about X, is

H(XjY) =Xy

P(Y = y)H(XjY = y);

where the summation index y ranges over all values of Y .

2.44 Fact (properties of conditional entropy) Let X and Y be random variables.

(i) The quantity H(XjY ) measures the amount of uncertainty remaining about X after

Y has been observed.

(ii) H(XjY ) _ 0 and H(XjX) = 0.

(iii) H(X; Y ) = H(X) + H(Y jX) = H(Y ) + H(XjY ).

(iv) H(XjY ) _ H(X), with equality if and only if X and Y are independent.

2.2.2 Mutual information

2.45 Definition The mutual information or transinformation of random variables X and Y is

I(X; Y) = H(X) - H(XjY ). Similarly, the transinformation of X and the pair Y , Z is

defined to be I(X; Y;Z) = H(X) - H(XjY;Z).

2.46 Fact (properties of mutual transinformation)

(i) The quantity I(X; Y ) can be thought of as the amount of information that Y reveals

about X. Similarly, the quantity I(X; Y;Z) can be thought of as the amount of information

that Y and Z together reveal about X.

(ii) I(X; Y ) _ 0.

(iii) I(X; Y) = 0 if and only if X and Y are independent (that is, Y contributes no information

about X).

(iv) I(X; Y) = I(Y ;X).

2.47 Definition The conditional transinformation of the pair X, Y given Z is defined to be

IZ(X; Y) = H(XjZ) - H(XjY;Z).

2.48 Fact (properties of conditional transinformation)

(i) The quantity IZ(X; Y ) can be interpreted as the amount of information that Y provides

about X, given that Z has already been observed.

(ii) I(X; Y;Z) = I(X; Y ) + IY (X;Z).

(iii) IZ(X; Y) = IZ(Y ;X).

2.3 Complexity theory

2.3.1 Basic definitions

Themain goal of complexity theory is to provide mechanisms for classifying computational

problems according to the resources needed to solve them. The classification should not

depend on a particular computational model, but rather should measure the intrinsic dif-

ficulty of the problem. The resources measured may include time, storage space, random

bits, number of processors, etc., but typically the main focus is time, and sometimes space.

2.49 Definition An algorithm is a well-defined computational procedure that takes a variable

input and halts with an output.

Of course, the term “well-defined computational procedure” is not mathematically precise.

It can be made so by using formal computational models such as Turing machines,

random-access machines, or boolean circuits. Rather than get involved with the technical

intricacies of these models, it is simpler to think of an algorithm as a computer program

written in some specific programming language for a specific computer that takes a variable

input and halts with an output.

It is usually of interest to find the most efficient (i.e., fastest) algorithm for solving a

given computational problem. The time that an algorithmtakes to halt depends on the “size”

of the probleminstance. Also, the unit of time used should bemade precise, especiallywhen

comparing the performance of two algorithms.

2.50 Definition The size of the input is the total number of bits needed to represent the input

in ordinary binary notation using an appropriate encoding scheme. Occasionally, the size

of the input will be the number of items in the input.

2.51 Example (sizes of some objects)

(i) The number of bits in the binary representation of a positive integer n is 1 + blg nc

bits. For simplicity, the size of n will be approximated by lg n.

(ii) If f is a polynomial of degree atmost k, each coefficient being a non-negative integer

at most n, then the size of f is (k + 1) lg n bits.

(iii) If A is a matrix with r rows, s columns, and with non-negative integer entries each

at most n, then the size of A is rs lg n bits. _

2.52 Definition The running time of an algorithm on a particular input is the number of primitive

operations or “steps” executed.

Often a step is taken to mean a bit operation. For some algorithms it will be more convenient

to take step to mean something else such as a comparison, a machine instruction, a

machine clock cycle, a modular multiplication, etc.

2.53 Definition The worst-case running time of an algorithmis an upper bound on the running

time for any input, expressed as a function of the input size.

2.54 Definition The average-case running time of an algorithm is the average running time

over all inputs of a fixed size, expressed as a function of the input size.

2.3.2 Asymptotic notation

It is often difficult to derive the exact running time of an algorithm. In such situations one

is forced to settle for approximations of the running time, and usually may only derive the

asymptotic running time. That is, one studies how the running time of the algorithm increases

as the size of the input increases without bound.

In what follows, the only functions considered are those which are defined on the positive

integers and take on real values that are always positive fromsome point onwards. Let

f and g be two such functions.

2.55 Definition (order notation)

(i) (asymptotic upper bound) f(n) = O(g(n)) if there exists a positive constant c and a

positive integer n0 such that 0 _ f(n) _ cg(n) for all n _ n0.

(ii) (asymptotic lower bound) f(n) = (g(n)) if there exists a positive constant c and a

positive integer n0 such that 0 _ cg(n) _ f(n) for all n _ n0.

(iii) (asymptotic tight bound) f(n) = _(g(n)) if there exist positive constants c1 and c2,

and a positive integer n0 such that c1g(n) _ f(n) _ c2g(n) for all n _ n0.

(iv) (o-notation) f(n) = o(g(n)) if for any positive constantc > 0 there exists a constant

n0 > 0 such that 0 _ f(n) < cg(n) for all n _ n0.

Intuitively, f(n) = O(g(n)) means that f grows no faster asymptotically than g(n) to

within a constant multiple, while f(n) = (g(n)) means that f(n) grows at least as fast

asymptotically as g(n) to within a constant multiple. f(n) = o(g(n)) means that g(n) is an

upper bound for f(n) that is not asymptotically tight, or in other words, the function f(n)

becomes insignificant relative to g(n) as n gets larger. The expression o(1) is often used to

signify a function f(n) whose limit as n approaches1is 0.

2.56 Fact (properties of order notation) For any functions f(n), g(n), h(n), and l(n), the following

are true.

(i) f(n) = O(g(n)) if and only if g(n) = (f(n)).

(ii) f(n) = _(g(n)) if and only if f(n) = O(g(n)) and f(n) = (g(n)).

(iii) If f(n) = O(h(n)) and g(n) = O(h(n)), then (f + g)(n) = O(h(n)).

(iv) If f(n) = O(h(n)) and g(n) = O(l(n)), then (f _ g)(n) = O(h(n)l(n)).

(v) (reflexivity) f(n) = O(f(n)).

(vi) (transitivity) If f(n) = O(g(n)) and g(n) = O(h(n)), then f(n) = O(h(n)).

2.57 Fact (approximations of some commonly occurring functions)

(i) (polynomial function) If f(n) is a polynomial of degree k with positive leading term,

then f(n) = _(nk).

(ii) For any constant c > 0, logc n = _(lgn).

(iii) (Stirling’s formula) For all integers n _ 1,

2_n _n

e _n

_ n! _

2_n _n

e _n+(1=(12n))

Thus n! =

2_n _n

e _n _1+_( 1

n)_. Also, n! = o(nn) and n! = (2n).

(iv) lg(n!) = _(n lg n).

2.58 Example (comparative growth rates of some functions) Let _ and c be arbitrary constants

with 0 < _ < 1 < c. The following functions are listed in increasing order of their asymptotic

growth rates:

1 < ln lnn < lnn < exp(

ln n ln ln n) < n_ < nc < nlnn < cn < nn < ccn

: _

2.3.3 Complexity classes

2.59 Definition A polynomial-time algorithm is an algorithm whose worst-case running time

function is of the form O(nk), where n is the input size and k is a constant. Any algorithm

whose running time cannot be so bounded is called an exponential-time algorithm.

Roughly speaking, polynomial-time algorithms can be equated with good or efficient

algorithms, while exponential-time algorithms are considered inefficient. There are, however,

some practical situations when this distinction is not appropriate. When considering

polynomial-time complexity, the degree of the polynomial is significant. For example, even

though an algorithm with a running time of O(nln ln n), n being the input size, is asymptotically

slower that an algorithm with a running time of O(n100), the former algorithm may

be faster in practice for smaller values of n, especially if the constants hidden by the big-O

notation are smaller. Furthermore, in cryptography, average-case complexity is more important

than worst-case complexity — a necessary condition for an encryption scheme to

be considered secure is that the corresponding cryptanalysis problem is difficult on average

(or more precisely, almost always difficult), and not just for some isolated cases.

2.60 Definition A subexponential-time algorithm is an algorithm whose worst-case running

time function is of the form eo(n), where n is the input size.

A subexponential-time algorithmis asymptotically faster than an algorithmwhose running

time is fully exponential in the input size, while it is asymptotically slower than a

polynomial-time algorithm.

2.61 Example (subexponential running time) Let A be an algorithm whose inputs are either

elements of a finite field Fq (see x2.6), or an integer q. If the expected running time of A is

of the form

Lq[_; c] = O_exp _(c + o(1))(ln q)_(ln ln q)1-___; (2.3)

where c is a positive constant, and _ is a constant satisfying 0 < _ < 1, then A is a

subexponential-time algorithm. Observe that for _ = 0, Lq[0; c] is a polynomial in ln q,

while for _ = 1, Lq[1; c] is a polynomial in q, and thus fully exponential in ln q. _

For simplicity, the theory of computational complexity restricts its attention to decision

problems, i.e., problems which have either YES or NO as an answer. This is not too

restrictive in practice, as all the computational problems that will be encountered here can

be phrased as decision problems in such a way that an efficient algorithm for the decision

problem yields an efficient algorithm for the computational problem, and vice versa.

2.62 Definition The complexity class P is the set of all decision problems that are solvable in

polynomial time.

2.63 Definition The complexity class NP is the set of all decision problems for which a YES

answer can be verified in polynomial time given some extra information, called a certificate.

2.64 Definition The complexity class co-NP is the set of all decision problems for which a NO

answer can be verified in polynomial time using an appropriate certificate.

It must be emphasized that if a decision problem is in NP, itmay not be the case that the

certificate of a YES answer can be easily obtained; what is asserted is that such a certificate

does exist, and, if known, can be used to efficiently verify the YES answer. The same is

true of the NO answers for problems in co-NP.

2.65 Example (problem in NP) Consider the following decision problem:

COMPOSITES

INSTANCE: A positive integer n.

QUESTION: Is n composite? That is, are there integers a; b > 1 such that n = ab?

COMPOSITES belongs to NP because if an integer n is composite, then this fact can be

verified in polynomial time if one is given a divisor a of n, where 1 < a < n(the certificate

in this case consists of the divisor a). It is in fact also the case that COMPOSITES belongs

to co-NP. It is still unknown whether or not COMPOSITES belongs to P. _

2.66 Fact P _ NP and P _ co-NP.

The following are among the outstanding unresolved questions in the subject of complexity

theory:

1. Is P = NP?

2. Is NP = co-NP?

3. Is P = NP \ co-NP?

Most experts are of the opinion that the answer to each of the three questions is NO, although

nothing along these lines has been proven.

The notion of reducibility is useful when comparing the relative difficulties of problems.

2.67 Definition Let L1 and L2 be two decision problems. L1 is said to polytime reduce to L2,

written L1 _P L2, if there is an algorithm that solves L1 which uses, as a subroutine, an

algorithm for solving L2, and which runs in polynomial time if the algorithm for L2 does.

Informally, if L1 _P L2, then L2 is at least as difficult as L1, or, equivalently, L1 is

no harder than L2.

2.68 Definition Let L1 and L2 be two decision problems. If L1 _P L2 and L2 _P L1, then

L1 and L2 are said to be computationally equivalent.

2.69 Fact Let L1, L2, and L3 be three decision problems.

(i) (transitivity) If L1 _P L2 and L2 _P L3, then L1 _P L3.

(ii) If L1 _P L2 and L2 2 P, then L1 2 P.

2.70 Definition A decision problem L is said to be NP-complete if

(i) L 2 NP, and

(ii) L1 _P L for every L1 2 NP.

The class of all NP-complete problems is denoted by NPC.

NP-complete problems are the hardest problems in NP in the sense that they are at

least as difficult as every other problem in NP. There are thousands of problems drawn from

diverse fields such as combinatorics, number theory, and logic, that are known to be NPcomplete.

2.71 Example (subset sum problem) The subset sum problem is the following: given a set of

positive integers fa1; a2; : : : ; ang and a positive integer s, determine whether or not there

is a subset of the ai that sum to s. The subset sum problem is NP-complete. _

2.72 Fact Let L1 and L2 be two decision problems.

(i) If L1 is NP-complete and L1 2 P, then P = NP.

(ii) If L1 2 NP, L2 is NP-complete, and L2 _P L1, then L1 is also NP-complete.

(iii) If L1 is NP-complete and L1 2 co-NP, then NP = co-NP.

By Fact 2.72(i), if a polynomial-time algorithm is found for any single NP-complete

problem, then it is the case that P = NP, a result that would be extremely surprising. Hence,

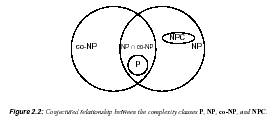
a proof that a problem is NP-complete provides strong evidence for its intractability. Figure

2.2 illustrates what is widely believed to be the relationship between the complexity

classes P, NP, co-NP, and NPC.

Fact 2.72(ii) suggests the following procedure for proving that a decision problem L1

is NP-complete:

1. Prove that L1 2 NP.

2. Select a problem L2 that is known to be NP-complete.

3. Prove that L2 _P L1.

2.73 Definition Aproblem isNP-hard if there exists someNP-complete problemthat polytime

reduces to it.

Note that the NP-hard classification is not restricted to only decision problems. Observe

also that an NP-complete problem is also NP-hard.

2.74 Example (NP-hard problem) Given positive integers a1; a2; : : : ; an and a positive integer

s, the computational version of the subset sum problem would ask to actually find a

subset of the ai which sums to s, provided that such a subset exists. This problem is NPhard.

2.3.4 Randomized algorithms

The algorithms studied so far in this section have been deterministic; such algorithms follow

the same execution path (sequence of operations) each time they execute with the same

input. By contrast, a randomized algorithm makes random decisions at certain points in

the execution; hence their execution paths may differ each time they are invoked with the

same input. The random decisions are based upon the outcome of a random number generator.

Remarkably, there are many problems for which randomized algorithms are known

that are more efficient, both in terms of time and space, than the best known deterministic

algorithms.

Randomized algorithms for decision problems can be classified according to the probability

that they return the correct answer.

2.75 Definition Let A be a randomized algorithm for a decision problem L, and let I denote

an arbitrary instance of L.

(i) A has 0-sided error if P(A outputs YES j I’s answer is YES ) = 1, and

P(A outputs YES j I’s answer is NO ) = 0.

(ii) A has 1-sided error if P(A outputs YES j I’s answer is YES ) _ 1

2, and

P(A outputs YES j I’s answer is NO ) = 0.

(iii) A has 2-sided error if P(A outputs YES j I’s answer is YES ) _ 2

3, and

P(A outputs YES j I’s answer is NO ) _ 1

3 .

The number 1

2 in the definition of 1-sided error is somewhat arbitrary and can be replaced

by any positive constant. Similarly, the numbers 2

3 and 1

3 in the definition of 2-sided

error, can be replaced by 1

2 + _ and 1

2 - _, respectively, for any constant _, 0 < _ < 1

2 .

2.76 Definition The expected running time of a randomized algorithmis an upper bound on the

expected running time for each input (the expectation being over all outputs of the random

number generator used by the algorithm), expressed as a function of the input size.

The important randomized complexity classes are defined next.

2.77 Definition (randomized complexity classes)

(i) The complexity class ZPP (“zero-sided probabilistic polynomial time”) is the set of

all decision problems for which there is a randomized algorithm with 0-sided error

which runs in expected polynomial time.

(ii) The complexity class RP (“randomized polynomial time”) is the set of all decision

problems for which there is a randomized algorithm with 1-sided error which runs in

(worst-case) polynomial time.

(iii) The complexity class BPP (“bounded error probabilistic polynomial time”) is the set

of all decision problems for which there is a randomized algorithm with 2-sided error

which runs in (worst-case) polynomial time.

2.78 Fact P _ ZPP _ RP _ BPP and RP _ NP.

2.4 Number theory

2.4.1 The integers

The set of integers f: : : ;-3;-2;-1; 0; 1; 2; 3; : : :g is denoted by the symbol Z.

2.79 Definition Let a, b be integers. Then a divides b (equivalently: a is a divisor of b, or a is

a factor of b) if there exists an integer c such that b = ac. If a divides b, then this is denoted

by ajb.

2.80 Example (i) -3j18, since 18 = (-3)(-6). (ii) 173j0, since 0 = (173)(0). _

The following are some elementary properties of divisibility.

2.81 Fact (properties of divisibility) For all a, b, c 2 Z, the following are true:

(i) aja.

(ii) If ajb and bjc, then ajc.

(iii) If ajb and ajc, then aj(bx + cy) for all x; y 2 Z.

(iv) If ajb and bja, then a = _b.

2.82 Definition (division algorithm for integers) If a and b are integers with b _ 1, then ordinary

long division of a by b yields integers q (the quotient) and r (the remainder) such

that

a = qb + r; where 0 _ r < b:

Moreover, q and r are unique. The remainder of the division is denoted a mod b, and the

quotient is denoted a div b.

2.83 Fact Let a; b 2 Z with b 6= 0. Then a div b = ba=bc and a mod b = a - bba=bc.

2.84 Example If a = 73, b = 17, then q = 4 and r = 5. Hence 73 mod 17 = 5 and

73 div 17 = 4. _

2.85 Definition An integer c is a common divisor of a and b if cja and cjb.

2.86 Definition A non-negative integer d is the greatest common divisor of integers a and b,

denoted d = gcd(a; b), if

(i) d is a common divisor of a and b; and

(ii) whenever cja and cjb, then cjd.

Equivalently, gcd(a; b) is the largest positive integer that divides both a and b, with the exception

that gcd(0; 0) = 0.

2.87 Example The common divisors of 12 and 18 aref_1;_2;_3;_6g, and gcd(12; 18) = 6.

2.88 Definition A non-negative integer d is the least common multiple of integers a and b, denoted

d = lcm(a; b), if

(i) ajd and bjd; and

(ii) whenever ajc and bjc, then djc.

Equivalently, lcm(a; b) is the smallest non-negative integer divisible by both a and b.

2.89 Fact If a and b are positive integers, then lcm(a; b) = a _ b= gcd(a; b).

2.90 Example Since gcd(12; 18) = 6, it follows that lcm(12; 18) = 12 _ 18=6 = 36. _

2.91 Definition Two integers a and b are said to be relatively prime or coprime if gcd(a; b) = 1.

2.92 Definition An integer p _ 2 is said to be prime if its only positive divisors are 1 and p.

Otherwise, p is called composite.

The following are some well known facts about prime numbers.

2.93 Fact If p is prime and pjab, then either pja or pjb (or both).

2.94 Fact There are an infinite number of prime numbers.

2.95 Fact (prime number theorem) Let _(x) denote the number of prime numbers _ x. Then

lim

x!1

_(x)

x= ln x

= 1:

This means that for large values of x, _(x) is closely approximated by the expression

x= ln x. For instance, when x = 1010, _(x) = 455; 052; 511, whereas bx= ln xc =

434; 294; 481. A more explicit estimate for _(x) is given below.

2.96 Fact Let _(x) denote the number of primes _ x. Then for x _ 17

_(x) >

ln x

and for x > 1

_(x) < 1:25506

lnx

2.97 Fact (fundamental theorem of arithmetic) Every integer n _ 2 has a factorization as a

product of prime powers:

n = pe1

1 pe2

2 _ _ _ pek

k ;

where the pi are distinct primes, and the ei are positive integers. Furthermore, the factorization

is unique up to rearrangement of factors.

2.98 Fact If a = pe1

1 pe2

2 _ _ _ pek

k , b = pf1

1 pf2

2 _ _ _ pfk

k , where each ei _ 0 and fi _ 0, then

gcd(a; b) = pmin(e1;f1)

1 pmin(e2;f2)

2 _ _ _ pmin(ek;fk)

and

lcm(a; b) = pmax(e1;f1)

1 pmax(e2;f2)

2 _ _ _ pmax(ek;fk)

k :

2.99 Example Let a = 4864 = 28 _ 19, b = 3458 = 2 _ 7 _ 13 _ 19. Then gcd(4864; 3458) =

2 _ 19 = 38 and lcm(4864; 3458) = 28 _ 7 _ 13 _ 19 = 442624. _

2.100 Definition For n _ 1, let _(n) denote the number of integers in the interval [1; n] which

are relatively prime to n. The function _ is called the Euler phi function (or the Euler totient

function).

2.101 Fact (properties of Euler phi function)

(i) If p is a prime, then _(p) = p - 1.

(ii) The Euler phi function is multiplicative. That is, if gcd(m; n) = 1, then _(mn) =

_(m) _ _(n).

(iii) If n = pe1

1 pe2

2 _ _ _ pek

k is the prime factorization of n, then

_(n) = n_1 -

p1__1 -

p2__ _ __1 -

pk _:

Fact 2.102 gives an explicit lower bound for _(n).

2.102 Fact For all integers n _ 5,

_(n) >

6 lnlnn