This is a Chapter from the Handbook of Applied Cryptography, by A. Menezes, P. van

Oorschot, and S. Vanstone, CRC Press, 1996.

For further information, see www.cacr.math.uwaterloo.ca/hac

CRC Press has granted the following speci_c permissions for the electronic version of this

book:

Permission is granted to retrieve, print and store a single copy of this chapter for

personal use. This permission does not extend to binding multiple chapters of

the book, photocopying or producing copies for other than personal use of the

person creating the copy, or making electronic copies available for retrieval by

others without prior permission in writing from CRC Press.

Except where over-ridden by the speci_c permission above, the standard copyright notice

from CRC Press applies to this electronic version:

Neither this book nor any part may be reproduced or transmitted in any form or

by any means, electronic or mechanical, including photocopying, micro_lming,

and recording, or by any information storage or retrieval system, without prior

permission in writing from the publisher.

The consent of CRC Press does not extend to copying for general distribution,

for promotion, for creating new works, or for resale. Speci_c permission must be

obtained in writing from CRC Press for such copying.

c 1997 by CRC Press, Inc.

1

Overview of Cryptography

Contents in Brief

1.1 Introduction : : : : : : : : : : : : : : : : : : : : : : : : : : : : : 1

1.2 Information security and cryptography : : : : : : : : : : : : : : 2

1.3 Background on functions : : : : : : : : : : : : : : : : : : : : : : 6

1.4 Basic terminology and concepts : : : : : : : : : : : : : : : : : : : 11

1.5 Symmetric-key encryption : : : : : : : : : : : : : : : : : : : : : 15

1.6 Digital signatures : : : : : : : : : : : : : : : : : : : : : : : : : : 22

1.7 Authentication and identification : : : : : : : : : : : : : : : : : : 24

1.8 Public-key cryptography : : : : : : : : : : : : : : : : : : : : : : 25

1.9 Hash functions : : : : : : : : : : : : : : : : : : : : : : : : : : : 33

1.10 Protocols and mechanisms : : : : : : : : : : : : : : : : : : : : : 33

1.11 Key establishment, management, and certification : : : : : : : : : 35

1.12 Pseudorandom numbers and sequences : : : : : : : : : : : : : : 39

1.13 Classes of attacks and security models : : : : : : : : : : : : : : : 41

1.14 Notes and further references : : : : : : : : : : : : : : : : : : : : 45

1.1 Introduction

Cryptography has a long and fascinating history. The most complete non-technical account

of the subject is Kahn’s The Codebreakers. This book traces cryptography from its initial

and limited use by the Egyptians some 4000 years ago, to the twentieth century where it

played a crucial role in the outcome of both world wars. Completed in 1963, Kahn’s book

covers those aspects of the historywhichwere most significant (up to that time) to the development

of the subject. The predominant practitioners of the art were those associated with

the military, the diplomatic service and government in general. Cryptography was used as

a tool to protect national secrets and strategies.

The proliferation of computers and communications systems in the 1960s brought with

it a demand from the private sector for means to protect information in digital form and to

provide security services. Beginning with the work of Feistel at IBMin the early 1970s and

culminating in 1977 with the adoption as a U.S. Federal Information Processing Standard

for encrypting unclassified information, DES, the Data Encryption Standard, is the most

well-known cryptographic mechanism in history. It remains the standard means for securing

electronic commerce for many financial institutions around the world.

Themost striking development in the history of cryptographycame in 1976whenDiffie

and Hellman published New Directions in Cryptography. This paper introduced the revolutionary

concept of public-key cryptography and also provided a new and ingenious method

for key exchange, the security of which is based on the intractability of the discrete logarithm

problem. Although the authors had no practical realization of a public-key encryption

scheme at the time, the idea was clear and it generated extensive interest and activity

in the cryptographic community. In 1978 Rivest, Shamir, and Adleman discovered the first

practical public-key encryption and signature scheme, now referred to as RSA. The RSA

scheme is based on another hard mathematical problem, the intractability of factoring large

integers. This application of a hard mathematical problem to cryptography revitalized efforts

to find more efficient methods to factor. The 1980s saw major advances in this area

but nonewhich rendered the RSA systeminsecure. Another class of powerful and practical

public-key schemes was found by ElGamal in 1985. These are also based on the discrete

logarithm problem.

One of the most significant contributions provided by public-key cryptography is the

digital signature. In 1991 the first international standard for digital signatures (ISO/IEC

9796) was adopted. It is based on the RSA public-key scheme. In 1994 the U.S. Government

adopted the Digital Signature Standard, a mechanism based on the ElGamal publickey

scheme.

The search for new public-key schemes, improvements to existing cryptographicmechanisms,

and proofs of security continues at a rapid pace. Various standards and infrastructures

involving cryptography are being put in place. Security products are being developed

to address the security needs of an information intensive society.

The purpose of this book is to give an up-to-date treatise of the principles, techniques,

and algorithms of interest in cryptographic practice. Emphasis has been placed on those

aspects which are most practical and applied. The reader will be made aware of the basic

issues and pointed to specific related research in the literature where more indepth discussions

can be found. Due to the volume of material which is covered, most results will be

stated without proofs. This also serves the purpose of not obscuring the very applied nature

of the subject. This book is intended for both implementers and researchers. It describes

algorithms, systems, and their interactions.

Chapter 1 is a tutorial on the many and various aspects of cryptography. It does not

attempt to convey all of the details and subtleties inherent to the subject. Its purpose is to

introduce the basic issues and principles and to point the reader to appropriate chapters in the

book for more comprehensive treatments. Specific techniques are avoided in this chapter.

1.2 Information security and cryptography

The concept of information will be taken to be an understood quantity. To introduce cryptography,

an understanding of issues related to information security in general is necessary.

Information security manifests itself in many ways according to the situation and requirement.

Regardless of who is involved, to one degree or another, all parties to a transaction

must have confidence that certain objectives associated with information security have been

met. Some of these objectives are listed in Table 1.1.

Over the centuries, an elaborate set of protocols and mechanisms has been created to

deal with information security issues when the information is conveyed by physical documents.

Often the objectives of information security cannot solely be achieved through

mathematical algorithms and protocols alone, but require procedural techniques and abidance

of laws to achieve the desired result. For example, privacy of letters is provided by

sealed envelopes delivered by an accepted mail service. The physical security of the envelope

is, for practical necessity, limited and so laws are enacted which make it a criminal

c 1997 by CRC Press, Inc.—See accompanying notice at front of chapter.

x 1.2 Information security and cryptography 3

privacy

or confidentiality

keeping information secret from all but those who are authorized

to see it.

data integrity ensuring information has not been altered by unauthorized or

unknown means.

entity authentication

or identification

corroboration of the identity of an entity (e.g., a person, a

computer terminal, a credit card, etc.).

message

authentication

corroborating the source of information; also known as data

origin authentication.

signature a means to bind information to an entity.

authorization conveyance, to another entity, of official sanction to do or be

something.

validation a means to provide timeliness of authorization to use or manipulate

information or resources.

access control restricting access to resources to privileged entities.

certification endorsement of information by a trusted entity.

timestamping recording the time of creation or existence of information.

witnessing verifying the creation or existence of information by an entity

other than the creator.

receipt acknowledgement that information has been received.

confirmation acknowledgement that services have been provided.

ownership a means to provide an entity with the legal right to use or

transfer a resource to others.

anonymity concealing the identity of an entity involved in some process.

non-repudiation preventing the denial of previous commitments or actions.

revocation retraction of certification or authorization.

Table 1.1:Some information security objectives.

offense to open mail for which one is not authorized. It is sometimes the case that security

is achieved not through the information itself but through the physical document recording

it. For example, paper currency requires special inks andmaterial to prevent counterfeiting.

Conceptually, the way information is recorded has not changed dramatically over time.

Whereas information was typically stored and transmitted on paper, much of it now resides

on magnetic media and is transmitted via telecommunications systems, some wireless.

What has changed dramatically is the ability to copy and alter information. One can

make thousands of identical copies of a piece of information stored electronically and each

is indistinguishable from the original. With information on paper, this is much more diffi-

cult. What is needed then for a society where information is mostly stored and transmitted

in electronic form is a means to ensure information security which is independent of the

physical medium recording or conveying it and such that the objectives of information security

rely solely on digital information itself.

One of the fundamental tools used in information security is the signature. It is a building

block formany other services such as non-repudiation, data origin authentication, identification,

and witnessing, to mention a few. Having learned the basics in writing, an individual

is taught how to produce a handwritten signature for the purpose of identification.

At contract age the signature evolves to take on a very integral part of the person’s identity.

This signature is intended to be unique to the individual and serve as a means to identify,

authorize, and validate. With electronic information the concept of a signature needs to be

Handbook of Applied Cryptography by A. Menezes, P. van Oorschot and S. Vanstone.

redressed; it cannot simply be something unique to the signer and independent of the information

signed. Electronic replication of it is so simple that appending a signature to a

document not signed by the originator of the signature is almost a triviality.

Analogues of the “paper protocols” currently in use are required. Hopefully these new

electronic based protocols are at least as good as those they replace. There is a unique opportunity

for society to introduce new and more efficient ways of ensuring information security.

Much can be learned from the evolution of the paper based system, mimicking those

aspects which have served us well and removing the inefficiencies.

Achieving information security in an electronic society requires a vast array of technical

and legal skills. There is, however, no guarantee that all of the information security objectives

deemed necessary can be adequately met. The technical means is provided through

cryptography.

1.1 Definition Cryptography is the study of mathematical techniques related to aspects of information

security such as confidentiality, data integrity, entity authentication, and data origin

authentication.

Cryptography is not the only means of providing information security, but rather one set of

techniques.

Cryptographic goals

Of all the information security objectives listed in Table 1.1, the following four form a

framework upon which the others will be derived: (1) privacy or confidentiality (x1.5, x1.8);

(2) data integrity (x1.9); (3) authentication (x1.7); and (4) non-repudiation (x1.6).

1. Confidentiality is a service used to keep the content of information from all but those

authorized to have it. Secrecy is a term synonymous with confidentiality and privacy.

There are numerous approaches to providing confidentiality, ranging from physical

protection to mathematical algorithms which render data unintelligible.

2. Data integrity is a service which addresses the unauthorized alteration of data. To

assure data integrity, one must have the ability to detect data manipulation by unauthorized

parties. Data manipulation includes such things as insertion, deletion, and

substitution.

3. Authentication is a service related to identification. This function applies to both entities

and information itself. Two parties entering into a communication should identify

each other. Information delivered over a channel should be authenticated as to origin,

date of origin, data content, time sent, etc. For these reasons this aspect of cryptography

is usually subdivided into two major classes: entity authentication and data

origin authentication. Data origin authentication implicitly provides data integrity

(for if a message is modified, the source has changed).

4. Non-repudiation is a service which prevents an entity fromdenying previous commitments

or actions. When disputes arise due to an entity denying that certain actions

were taken, a means to resolve the situation is necessary. For example, one entity

may authorize the purchase of property by another entity and later deny such authorization

was granted. A procedure involving a trusted third party is needed to resolve

the dispute.

A fundamental goal of cryptography is to adequately address these four areas in both

theory and practice. Cryptography is about the prevention and detection of cheating and

other malicious activities.

This book describes a number of basic cryptographic tools (primitives) used to provide

information security. Examples of primitives include encryption schemes (x1.5 and x1.8),

hash functions (x1.9), and digital signature schemes (x1.6). Figure 1.1 provides a schematic

listing of the primitives considered and how they relate. Many of these will be briefly introduced

in this chapter, with detailed discussion left to later chapters. These primitives should

be evaluated with respect to various criteria such as:

1. level of security. This is usually difficult to quantify. Often it is given in terms of the

number of operations required (using the best methods currently known) to defeat the

intended objective. Typically the level of security is defined by an upper bound on

the amount of work necessary to defeat the objective. This is sometimes called the

work factor (see x1.13.4).

2. functionality. Primitives will need to be combined to meet various information security

objectives. Which primitives are most effective for a given objective will be

determined by the basic properties of the primitives.

3. methods of operation. Primitives, when applied in various ways and with various inputs,

will typically exhibit different characteristics; thus, one primitive could provide

very different functionality depending on its mode of operation or usage.

4. performance. This refers to the efficiency of a primitive in a particular mode of operation.

(For example, an encryption algorithm may be rated by the number of bits

per second which it can encrypt.)

5. ease of implementation. This refers to the difficulty of realizing the primitive in a

practical instantiation. This might include the complexity of implementing the primitive

in either a software or hardware environment.

The relative importance of various criteria is very much dependent on the application

and resources available. For example, in an environmentwhere computing power is limited

one may have to trade off a very high level of security for better performance of the system

as a whole.

Cryptography, over the ages, has been an art practised by many who have devised ad

hoc techniques to meet some of the information security requirements. The last twenty

years have been a period of transition as the disciplinemoved froman art to a science. There

are now several international scientific conferences devoted exclusively to cryptography

and also an international scientific organization, the International Association for Cryptologic

Research (IACR), aimed at fostering research in the area.

This book is about cryptography: the theory, the practice, and the standards.

1.3 Background on functions

While this book is not a treatise on abstract mathematics, a familiarity with basic mathematical

concepts will prove to be useful. One concept which is absolutely fundamental to

cryptography is that of a function in the mathematical sense. A function is alternately referred

to as a mapping or a transformation.

1.3.1 Functions (1-1, one-way, trapdoor one-way)

A set consists of distinct objects which are called elements of the set. For example, a set X

might consist of the elements a, b, c, and this is denoted X = fa; b; cg.

1.2 Definition A function is defined by two sets X and Y and a rule f which assigns to each

element in X precisely one element in Y . The set X is called the domain of the function

and Y the codomain. If x is an element of X (usually written x 2 X) the image of x is the

element in Y which the rule f associates with x; the image y of x is denoted by y = f(x).

Standard notation for a function f from set X to set Y is f : X -! Y . If y 2 Y , then a

preimage of y is an element x 2 X for which f(x) = y. The set of all elements in Y which

have at least one preimage is called the image of f, denoted Im(f).

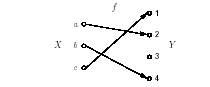
1.3 Example (function) Consider the sets X = fa; b; cg, Y = f1; 2; 3; 4g, and the rule f

from X to Y defined as f(a) = 2, f(b) = 4, f(c) = 1. Figure 1.2 shows a schematic of

the sets X, Y and the function f. The preimage of the element 2 is a. The image of f is

f1; 2; 4g. _

Thinking of a function in terms of the schematic (sometimes called a functional diagram)

given in Figure 1.2, each element in the domain X has precisely one arrowed line

originating from it. Each element in the codomain Y can have any number of arrowed lines

incident to it (including zero lines).

c 1997 by CRC Press, Inc.—See accompanying notice at front of chapter.

Often only the domain X and the rule f are given and the codomain is assumed to be

the image of f. This point is illustrated with two examples.

1.4 Example (function) TakeX = f1; 2; 3; : : : ; 10g and let f be the rule that for each x 2 X,

f(x) = rx, where rx is the remainder when x2 is divided by 11. Explicitly then

f(1) = 1 f(2) = 4 f(3) = 9 f(4) = 5 f(5) = 3

f(6) = 3 f(7) = 5 f(8) = 9 f(9) = 4 f(10) = 1:

The image of f is the set Y = f1; 3; 4; 5; 9g. _

1.5 Example (function) TakeX = f1; 2; 3; : : : ; 1050g and let f be the rule f(x) = rx, where

rx is the remainder when x2 is divided by 1050 + 1 for all x 2 X. Here it is not feasible

to write down f explicitly as in Example 1.4, but nonetheless the function is completely

specified by the domain and the mathematical description of the rule f. _

(i) 1-1 functions

1.6 Definition A function (or transformation) is 1 - 1 (one-to-one) if each element in the

codomain Y is the image of at most one element in the domain X.

1.7 Definition A function (or transformation) is onto if each element in the codomain Y is

the image of at least one element in the domain. Equivalently, a function f : X -! Y is

onto if Im(f) = Y .

1.8 Definition If a function f : X -! Y is 1-1 and Im(f) = Y , then f is called a bijection.

1.9 Fact If f : X -! Y is 1 - 1 then f : X -! Im(f) is a bijection. In particular, if

f : X -! Y is 1 - 1, and X and Y are finite sets of the same size, then f is a bijection.

In terms of the schematic representation, if f is a bijection, then each element in Y

has exactly one arrowed line incident with it. The functions described in Examples 1.3 and

1.4 are not bijections. In Example 1.3 the element 3 is not the image of any element in the

domain. In Example 1.4 each element in the codomain has two preimages.

1.10 Definition If f is a bijection fromX to Y then it is a simple matter to define a bijection g

from Y to X as follows: for each y 2 Y define g(y) = x where x 2 X and f(x) = y. This

function g obtained from f is called the inverse function of f and is denoted by g = f-1.

1.11 Example (inverse function) Let X = fa; b; c; d; eg, and Y = f1; 2; 3; 4; 5g, and consider

the rule f given by the arrowed edges in Figure 1.3. f is a bijection and its inverse g is

formed simply by reversing the arrows on the edges. The domain of g is Y and the codomain

is X. _

Note that if f is a bijection, then so is f-1. In cryptography bijections are used as

the tool for encrypting messages and the inverse transformations are used to decrypt. This

will be made clearer in x1.4 when some basic terminology is introduced. Notice that if the

transformations were not bijections then it would not be possible to always decrypt to a

unique message.

(ii) One-way functions

There are certain types of functions which play significant roles in cryptography. At the

expense of rigor, an intuitive definition of a one-way function is given.

1.12 Definition A function f from a set X to a set Y is called a one-way function if f(x) is

“easy” to compute for all x 2 X but for “essentially all” elements y 2 Im(f) it is “computationally

infeasible” to find any x 2 X such that f(x) = y.

1.13 Note (clarification of terms in Definition 1.12)

(i) A rigorous definition of the terms “easy” and “computationally infeasible” is necessary

but would detract from the simple idea that is being conveyed. For the purpose

of this chapter, the intuitive meaning will suffice.

(ii) The phrase “for essentially all elements in Y ” refers to the fact that there are a few

values y 2 Y for which it is easy to find an x 2 X such that y = f(x). For example,

one may compute y = f(x) for a small number of x values and then for these, the

inverse is known by table look-up. An alternate way to describe this property of a

one-way function is the following: for a random y 2 Im(f) it is computationally

infeasible to find any x 2 X such that f(x) = y.

The concept of a one-way function is illustrated through the following examples.

1.14 Example (one-way function) Take X = f1; 2; 3; : : : ; 16g and define f(x) = rx for all

x 2 X where rx is the remainder when 3x is divided by 17. Explicitly,

x given that f(x) = 7. Of course, if the number you are given is 3 then it is clear that x = 1

is what you need; but for most of the elements in the codomain it is not that easy. _

One must keep in mind that this is an example which uses very small numbers; the

important point here is that there is a difference in the amount of work to compute f(x)

and the amount of work to find x given f(x). Even for very large numbers, f(x) can be

computed efficiently using the repeated square-and-multiply algorithm (Algorithm 2.143),

whereas the process of finding x from f(x) is much harder.

1.15 Example (one-way function) A prime number is a positive integer greater than 1 whose

only positive integer divisors are 1 and itself. Select primes p = 48611, q = 53993, form

n = pq = 2624653723, and let X = f1; 2; 3; : : : ; n - 1g. Define a function f on X

by f(x) = rx for each x 2 X, where rx is the remainder when x3 is divided by n. For

instance, f(2489991) = 1981394214 since 24899913 = 5881949859 _ n + 1981394214.

Computing f(x) is a relatively simple thing to do, but to reverse the procedure ismuchmore

difficult; that is, given a remainder to find the value x which was originally cubed (raised

to the third power). This procedure is referred to as the computation of a modular cube root

with modulus n. If the factors of n are unknown and large, this is a difficult problem; however,

if the factors p and q of n are known then there is an efficient algorithmfor computing

modular cube roots. (See x8.2.2(i) for details.) _

Example 1.15 leads one to consider another type of function which will prove to be

fundamental in later developments.

(iii) Trapdoor one-way functions

1.16 Definition A trapdoor one-way function is a one-way function f : X -! Y with the

additional property that given some extra information (called the trapdoor information) it

becomes feasible to find for any given y 2 Im(f), an x 2 X such that f(x) = y.

Example 1.15 illustrates the concept of a trapdoor one-way function. With the additional

information of the factors of n = 2624653723 (namely, p = 48611 and q = 53993,

each of which is five decimal digits long) it becomes much easier to invert the function.

The factors of 2624653723 are large enough that finding them by hand computation would

be difficult. Of course, any reasonable computer program could find the factors relatively

quickly. If, on the other hand, one selects p and q to be very large distinct prime numbers

(each having about 100 decimal digits) then, by today’s standards, it is a difficult problem,

even with the most powerful computers, to deduce p and q simply from n. This is the wellknown

integer factorization problem (see x3.2) and a source of many trapdoor one-way

functions.

It remains to be rigorously established whether there actually are any (true) one-way

functions. That is to say, no one has yet definitively proved the existence of such functions

under reasonable (and rigorous) definitions of “easy” and “computationally infeasible”.

Since the existence of one-way functions is still unknown, the existence of trapdoor

one-way functions is also unknown. However, there are a number of good candidates for

one-way and trapdoor one-way functions. Many of these are discussed in this book, with

emphasis given to those which are practical.

One-way and trapdoor one-way functions are the basis for public-key cryptography

(discussed in x1.8). The importance of these concepts will become clearer when their application

to cryptographic techniques is considered. It will be worthwhile to keep the abstract

concepts of this section in mind as concrete methods are presented.

1.3.2 Permutations

Permutations are functions which are often used in various cryptographic constructs.

1.17 Definition Let S be a finite set of elements. A permutation p on S is a bijection (Definition

1.8) from S to itself (i.e., p: S -!S).

1.18 Example (permutation) Let S = f1; 2; 3; 4; 5g. A permutation p: S -!S is defined as

follows:

p(1) = 3; p(2) = 5; p(3) = 4; p(4) = 2; p(5) = 1:

Apermutation can be described in variousways. It can be displayed as above or as an array:

p = _ 1 2 3 4 5

3 5 4 2 1 _; (1.1)

where the top row in the array is the domain and the bottom row is the image under the

mapping p. Of course, other representations are possible. _

Since permutations are bijections, they have inverses. If a permutation is written as an

array (see 1.1), its inverse is easily found by interchanging the rows in the array and reordering

the elements in the new top row if desired (the bottom row would have to be reordered

correspondingly). The inverse of p in Example 1.18 is p-1 = _ 1 2 3 4 5

5 4 1 3 2 _:

1.19 Example (permutation) Let X be the set of integers f0; 1; 2; : : : ; pq - 1g where p and q

are distinct large primes (for example, p and q are each about 100 decimal digits long), and

suppose that neither p-1 nor q-1 is divisible by 3. Then the function p(x) = rx, where rx

is the remainder when x3 is divided by pq, can be shown to be a permutation. Determining

the inverse permutation is computationally infeasible by today’s standards unless p and q

are known (cf. Example 1.15). _

1.3.3 Involutions

Another type of function which will be referred to in x1.5.3 is an involution. Involutions

have the property that they are their own inverses.

1.20 Definition Let S be a finite set and let f be a bijection from S to S (i.e., f : S -! S).

The function f is called an involution if f = f-1. An equivalent way of stating this is

f(f(x)) = x for all x 2 S.

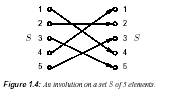
1.21 Example (involution) Figure 1.4 is an example of an involution. In the diagram of an

involution, note that if j is the image of i then i is the image of j. _

1.4 Basic terminology and concepts

The scientific study of any discipline must be built upon rigorous definitions arising from

fundamental concepts. What follows is a list of terms and basic concepts used throughout

this book. Where appropriate, rigor has been sacrificed (here in Chapter 1) for the sake of

clarity.

Encryption domains and codomains

_ Adenotes a finite set called the alphabet of definition. For example, A = f0; 1g, the

binary alphabet, is a frequently used alphabet of definition. Note that any alphabet

can be encoded in terms of the binary alphabet. For example, since there are 32 binary

strings of length five, each letter of the English alphabet can be assigned a unique

binary string of length five.

_ Mdenotes a set called the message space. Mconsists of strings of symbols from

an alphabet of definition. An element ofMis called a plaintext message or simply

a plaintext. For example,Mmay consist of binary strings, English text, computer

code, etc.

_ C denotes a set called the ciphertext space. C consists of strings of symbols from an

alphabet of definition, which may differ from the alphabet of definition forM. An

element of C is called a ciphertext.

Encryption and decryption transformations

_ Kdenotes a set called the key space. An element of K is called a key.

_ Each element e 2 K uniquely determines a bijection fromMto C, denoted by Ee.

Ee is called an encryption function or an encryption transformation. Note that Ee

must be a bijection if the process is to be reversed and a unique plaintext message

recovered for each distinct ciphertext.1

_ For each d 2 K, Dd denotes a bijection from C toM(i.e., Dd : C -!M). Dd is

called a decryption function or decryption transformation.

_ The process of applying the transformation Ee to a message m 2 Mis usually referred

to as encrypting m or the encryption of m.

_ The process of applying the transformationDd to a ciphertext c is usually referred to

as decrypting c or the decryption of c.

1More generality is obtained if Ee is simply defined as a 1 - 1 transformation fromMto C. That is to say,

Ee is a bijection fromMto Im(Ee) where Im(Ee) is a subset of C.

_ An encryption scheme consists of a set fEe : e 2 Kg of encryption transformations

and a corresponding set fDd : d 2 Kg of decryption transformations with the property

that for each e 2 K there is a unique key d 2 K such that Dd = E-1

e ; that is,

Dd(Ee(m)) = m for all m 2 M. An encryption scheme is sometimes referred to

as a cipher.

_ The keys e and d in the preceding definition are referred to as a key pair and sometimes

denoted by (e; d). Note that e and d could be the same.

_ To construct an encryption scheme requires one to select a message spaceM, a ciphertext

space C, a key space K, a set of encryption transformations fEe : e 2 Kg,

and a corresponding set of decryption transformations fDd : d 2 Kg.

Achieving confidentiality

An encryption scheme may be used as follows for the purpose of achieving confidentiality.

Two parties Alice and Bob first secretly choose or secretly exchange a key pair (e; d). At a

subsequent point in time, if Alice wishes to send a message m2Mto Bob, she computes

c = Ee(m) and transmits this to Bob. Upon receiving c, Bob computes Dd(c) = m and

hence recovers the original message m.

The question arises as to why keys are necessary. (Why not just choose one encryption

function and its corresponding decryption function?) Having transformations which are

very similar but characterized by keys means that if some particular encryption/decryption

transformation is revealed then one does not have to redesign the entire scheme but simply

change the key. It is sound cryptographic practice to change the key (encryption/decryption

transformation) frequently. As a physical analogue, consider an ordinary resettable combination

lock. The structure of the lock is available to anyonewho wishes to purchase one but

the combination is chosen and set by the owner. If the owner suspects that the combination

has been revealed he can easily reset it without replacing the physical mechanism.

1.22 Example (encryption scheme) Let M = fm1;m2;m3g and C = fc1; c2; c3g. There

are precisely 3! = 6 bijections from M to C. The key space K = f1; 2; 3; 4; 5; 6g has

six elements in it, each specifying one of the transformations. Figure 1.5 illustrates the six

encryption functions which are denoted by Ei; 1 _ i _ 6. Alice and Bob agree on a trans-

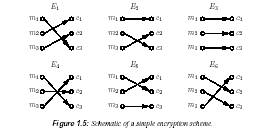
WhenMis a small set, the functional diagram is a simple visual means to describe the

mapping. In cryptography, the setMis typically of astronomical proportions and, as such,

the visual description is infeasible. What is required, in these cases, is some other simple

means to describe the encryption and decryption transformations, such as mathematical algorithms.

_

Figure 1.6 provides a simple model of a two-party communication using encryption.

Communication participants

Referring to Figure 1.6, the following terminology is defined.

_ An entity or party is someone or something which sends, receives, or manipulates

information. Alice and Bob are entities in Example 1.22. An entity may be a person,

a computer terminal, etc.

_ Asender is an entity in a two-party communicationwhich is the legitimate transmitter

of information. In Figure 1.6, the sender is Alice.

_ A receiver is an entity in a two-party communication which is the intended recipient

of information. In Figure 1.6, the receiver is Bob.

_ An adversary is an entity in a two-party communication which is neither the sender

nor receiver, andwhich tries to defeat the information security service being provided

between the sender and receiver. Various other names are synonymous with adversary

such as enemy, attacker, opponent, tapper, eavesdropper, intruder, and interloper.

An adversary will often attempt to play the role of either the legitimate sender or the

legitimate receiver.

Channels

_ A channel is a means of conveying information from one entity to another.

_ A physically secure channel or secure channel is one which is not physically accessible

to the adversary.

_ An unsecured channel is one from which parties other than those for which the information

is intended can reorder, delete, insert, or read.

_ Asecured channel is one fromwhich an adversary does not have the ability to reorder,

delete, insert, or read.

One should note the subtle difference between a physically secure channel and a secured

channel – a secured channelmay be secured by physical or cryptographic techniques,

the latter being the topic of this book. Certain channels are assumed to be physically secure.

These include trusted couriers, personal contact between communicating parties, and a dedicated

communication link, to name a few.

Security

A fundamental premise in cryptography is that the setsM; C;K; fEe : e 2 Kg, fDd : d 2

Kg are public knowledge. When two parties wish to communicate securely using an encryption

scheme, the only thing that they keep secret is the particular key pair (e; d) which

they are using, and which they must select. One can gain additional security by keeping the

class of encryption and decryption transformations secret but one should not base the security

of the entire scheme on this approach. History has shown that maintaining the secrecy

of the transformations is very difficult indeed.

1.23 Definition An encryption scheme is said to be breakable if a third party, without prior

knowledge of the key pair (e; d), can systematically recover plaintext from corresponding

ciphertext within some appropriate time frame.

An appropriate time frame will be a function of the useful lifespan of the data being

protected. For example, an instruction to buy a certain stockmay only need to be kept secret

for a few minutes whereas state secrets may need to remain confidential indefinitely.

An encryption scheme can be broken by trying all possible keys to see which one the

communicating parties are using (assuming that the class of encryption functions is public

knowledge). This is called an exhaustive search of the key space. It follows then that the

number of keys (i.e., the size of the key space) should be large enough to make this approach

computationally infeasible. It is the objective of a designer of an encryption scheme that this

be the best approach to break the system.

Frequently cited in the literature are Kerckhoffs’ desiderata, a set of requirements for

cipher systems. They are given here essentially as Kerckhoffs originally stated them:

1. the system should be, if not theoretically unbreakable, unbreakable in practice;

2. compromise of the system details should not inconvenience the correspondents;

3. the key should be rememberable without notes and easily changed;

4. the cryptogram should be transmissible by telegraph;

5. the encryption apparatus should be portable and operable by a single person; and

6. the system should be easy, requiring neither the knowledge of a long list of rules nor

mental strain.

This list of requirementswas articulated in 1883 and, for the most part, remains useful today.

Point 2 allows that the class of encryption transformations being used be publicly known

and that the security of the system should reside only in the key chosen.

Information security in general

So far the terminology has been restricted to encryption and decryption with the goal of privacy

in mind. Information security is much broader, encompassing such things as authentication

and data integrity. A few more general definitions, pertinent to discussions later in

the book, are given next.

_ An information security service is a method to provide some specific aspect of security.

For example, integrity of transmitted data is a security objective, and a method

to ensure this aspect is an information security service.

_ Breaking an information security service (which often involvesmore than simply encryption)

implies defeating the objective of the intended service.

_ A passive adversary is an adversarywho is capable only of reading information from

an unsecured channel.

_ An active adversary is an adversary who may also transmit, alter, or delete information

on an unsecured channel.

Cryptology

_ Cryptanalysis is the study of mathematical techniques for attempting to defeat cryptographic

techniques, and, more generally, information security services.

_ A cryptanalyst is someone who engages in cryptanalysis.

_ Cryptology is the study of cryptography (Definition 1.1) and cryptanalysis.

_ A cryptosystem is a general term referring to a set of cryptographic primitives used

to provide information security services. Most often the term is used in conjunction

with primitives providing confidentiality, i.e., encryption.

Cryptographic techniques are typically divided into two generic types: symmetric-key

and public-key. Encryptionmethods of these types will be discussed separately in x1.5 and

x1.8. Other definitions and terminology will be introduced as required.

1.5 Symmetric-key encryption

x1.5 considers symmetric-key encryption. Public-key encryption is the topic of x1.8.

1.5.1 Overview of block ciphers and stream ciphers

1.24 Definition Consider an encryption scheme consisting of the sets of encryption and decryption

transformations fEe : e 2 Kg and fDd : d 2 Kg, respectively, where K is the key

space. The encryption scheme is said to be symmetric-key if for each associated encryption/

decryption key pair (e; d), it is computationally “easy” to determine d knowing only e,

and to determine e from d.

Since e = d in most practical symmetric-key encryption schemes, the term symmetrickey

becomes appropriate. Other terms used in the literature are single-key, one-key, privatekey,

2 and conventional encryption. Example 1.25 illustrates the idea of symmetric-key encryption.

1.25 Example (symmetric-key encryption) Let A = fA;B;C; : : : ;X;Y; Zg be the English

alphabet. LetMand C be the set of all strings of length five over A. The key e is chosen

to be a permutation on A. To encrypt, an English message is broken up into groups each

having five letters (with appropriate padding if the length of the message is not a multiple

of five) and a permutation e is applied to each letter one at a time. To decrypt, the inverse

permutation d = e-1 is applied to each letter of the ciphertext. For instance, suppose that

the key e is chosen to be the permutation which maps each letter to the one which is three

positions to its right, as shown below

e = _A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

D E F G H I J K L M N O P Q R S T U V W X Y Z A B C_

2Private key is a term also used in quite a different context (see x1.8). The term will be reserved for the latter

usage in this book.

fidential and authentic) channel. One of the major issues with symmetric-key systems is to

find an efficientmethod to agree upon and exchange keys securely. This problem is referred

to as the key distribution problem (see Chapters 12 and 13).

It is assumed that all parties know the set of encryption/decryptiontransformations (i.e.,

they all know the encryption scheme). As has been emphasized several times the only information

which should be required to be kept secret is the key d. However, in symmetric-key

encryption, this means that the key e must also be kept secret, as d can be deduced from

e. In Figure 1.7 the encryption key e is transported from one entity to the other with the

understanding that both can construct the decryption key d.

There are two classes of symmetric-key encryption schemes which are commonly distinguished:

block ciphers and stream ciphers.

1.26 Definition A block cipher is an encryption scheme which breaks up the plaintext messages

to be transmitted into strings (called blocks) of a fixed length t over an alphabet A,

and encrypts one block at a time.

Most well-known symmetric-key encryption techniques are block ciphers. A number

of examples of these are given in Chapter 7. Two important classes of block ciphers are

substitution ciphers and transposition ciphers (x1.5.2). Product ciphers (x1.5.3) combine

these. Stream ciphers are considered in x1.5.4, while comments on the key space follow in

x1.5.5.

1.5.2 Substitution ciphers and transposition ciphers

Substitution ciphers are block ciphers which replace symbols (or groups of symbols) by

other symbols or groups of symbols.

Simple substitution ciphers

1.27 Definition Let A be an alphabet of q symbols andMbe the set of all strings of length

t over A. Let K be the set of all permutations on the set A. Define for each e 2 K an

encryption transformation Ee as:

Ee(m) = (e(m1)e(m2) _ _ _ e(mt)) = (c1c2 _ _ _ ct) = c;

where m = (m1m2 _ _ _mt) 2 M. In other words, for each symbol in a t-tuple, replace

(substitute) it by another symbol fromAaccording to some fixed permutation e. To decrypt

c = (c1c2 _ _ _ ct) compute the inverse permutation d = e-1 and

Dd(c) = (d(c1)d(c2) _ _ _ d(ct)) = (m1m2 _ _ _mt) = m:

Ee is called a simple substitution cipher or a mono-alphabetic substitution cipher.

The number of distinct substitution ciphers is q! and is independent of the block size in

the cipher. Example 1.25 is an example of a simple substitution cipher of block length five.

Simple substitution ciphers over small block sizes provide inadequate security even

when the key space is extremely large. If the alphabet is the English alphabet as in Example

1.25, then the size of the key space is 26! _ 4 _ 1026, yet the key being used can be

determined quite easily by examining a modest amount of ciphertext. This follows from the

simple observation that the distribution of letter frequencies is preserved in the ciphertext.

For example, the letter E occurs more frequently than the other letters in ordinary English

text. Hence the letter occurring most frequently in a sequence of ciphertext blocks is most

likely to correspond to the letter E in the plaintext. By observing a modest quantity of ciphertext

blocks, a cryptanalyst can determine the key.

Homophonic substitution ciphers

1.28 Definition To each symbol a 2 A, associate a set H(a) of strings of t symbols, with

the restriction that the sets H(a), a 2 A, be pairwise disjoint. A homophonic substitution

cipher replaces each symbol a in a plaintext message block with a randomly chosen string

from H(a). To decrypt a string c of t symbols, one must determine an a 2 A such that

c 2 H(a). The key for the cipher consists of the sets H(a).

1.29 Example (homophonic substitution cipher) Consider A = fa; bg, H(a) = f00; 10g, and

H(b) = f01; 11g. The plaintext message block ab encrypts to one of the following: 0001,

0011, 1001, 1011. Observe that the codomain of the encryption function (for messages of

length two) consists of the following pairwise disjoint sets of four-element bitstrings:

aa -! f0000; 0010; 1000; 1010g

ab -! f0001; 0011; 1001; 1011g

ba -! f0100; 0110; 1100; 1110g

bb -! f0101; 0111; 1101; 1111g

Often the symbols do not occur with equal frequency in plaintext messages. With a

simple substitution cipher this non-uniform frequency property is reflected in the ciphertext

as illustrated in Example 1.25. A homophonic cipher can be used to make the frequency of

occurrence of ciphertext symbols more uniform, at the expense of data expansion. Decryption

is not as easily performed as it is for simple substitution ciphers.

Polyalphabetic substitution ciphers

1.30 Definition A polyalphabetic substitution cipher is a block cipher with block length t over

an alphabet A having the following properties:

(i) the key space K consists of all ordered sets of t permutations (p1; p2; : : : ; pt), where

each permutation pi is defined on the set A;

(ii) encryption of the message m = (m1m2 _ _ _mt) under the key e = (p1; p2; : : : ; pt)

is given by Ee(m) = (p1(m1)p2(m2) _ _ _ pt(mt)); and

(iii) the decryption key associated with e = (p1; p2; : : : ; pt) is d = (p-1

1 ; p-1

2 ; : : : ; p-1

t ).

1.31 Example (Vigen`ere cipher) Let A = fA;B;C; : : : ;X;Y; Zg and t = 3. Choose e =

(p1; p2; p3), where p1 maps each letter to the letter three positions to its right in the alphabet,

p2 to the one seven positions to its right, and p3 ten positions to its right. If

m = THI SCI PHE RIS CER TAI NLY NOT SEC URE

then

c = Ee(m) = WOS VJS SOO UPC FLBWHS QSI QVD VLM XYO: _

Polyalphabetic ciphers have the advantage over simple substitution ciphers that symbol

frequencies are not preserved. In the example above, the letter E is encrypted to both O and

L. However, polyalphabetic ciphers are not significantly more difficult to cryptanalyze, the

approach being similar to the simple substitution cipher. In fact, once the block length t is

determined, the ciphertext letters can be divided into t groups (where group i, 1 _ i _ t,

consists of those ciphertext letters derived using permutation pi), and a frequency analysis

can be done on each group.

Transposition ciphers

Another class of symmetric-key ciphers is the simple transposition cipher, which simply

permutes the symbols in a block.

1.32 Definition Consider a symmetric-key block encryption scheme with block length t. LetK

be the set of all permutations on the set f1; 2; : : : ; tg. For each e 2 Kdefine the encryption

function

Ee(m) = (me(1)me(2) _ _ _me(t))

where m = (m1m2 _ _ _mt)2M, the message space. The set of all such transformations

is called a simple transposition cipher. The decryption key corresponding to e is the inverse

permutation d = e-1. To decrypt c = (c1c2 _ _ _ ct), computeDd(c) = (cd(1)cd(2) _ _ _ cd(t)).

A simple transposition cipher preserves the number of symbols of a given type within

a block, and thus is easily cryptanalyzed.

1.5.3 Composition of ciphers

In order to describe product ciphers, the concept of composition of functions is introduced.

Compositions are a convenient way of constructing more complicated functions from simpler

ones.

Composition of functions

1.33 Definition Let S, T , and U be finite sets and let f : S -!T and g : T -!U be functions.

The composition of g with f, denoted g _ f (or simply gf), is a function from S to

U as illustrated in Figure 1.8 and defined by (g _ f)(x) = g(f(x)) for all x 2 S.

Composition can be easily extended to more than two functions. For functions f1, f2,

: : : ; ft, one can define ft__ _ __f2 _f1, provided that the domain of ft equals the codomain

of ft-1 and so on.

Compositions and involutions

Involutionswere introduced in x1.3.3 as a simple class of functions with an interesting property:

Ek(Ek(x)) = x for all x in the domain of Ek; that is, Ek _Ek is the identity function.

1.34 Remark (composition of involutions) The composition of two involutions is not necessarily

an involution, as illustrated in Figure 1.9. However, involutions may be composed to get

somewhat more complicated functionswhose inverses are easy to find. This is an important

feature for decryption. For example if Ek1;Ek2; : : : ;Ekt are involutions then the inverse

of E = E E _ _ _E is E-1

= E E _ _ _E , the composition of the involutions

Product ciphers

Simple substitution and transposition ciphers individually do not provide a very high level

of security. However, by combining these transformations it is possible to obtain strong ciphers.

As will be seen in Chapter 7 some of the most practical and effective symmetric-key

systems are product ciphers. One example of a product cipher is a composition of t _ 2

transformations Ek1Ek2 _ _ _Ekt where each Eki , 1 _ i _ t, is either a substitution or a

transposition cipher. For the purpose of this introduction, let the composition of a substitution

and a transposition be called a round.

1.35 Example (product cipher) LetM= C = K be the set of all binary strings of length six.

The number of elements inMis 26 = 64. Let m = (m1m2 _ _ _m6) and define

E(1)

k (m) = m_ k; where k 2 K;

E(2)(m) = (m4m5m6m1m2m3):

Here, _ is the exclusive-OR (XOR) operation defined as follows: 0 _ 0 = 0, 0 _ 1 = 1,

1 _ 0 = 1, 1 _ 1 = 0. E(1)

k is a polyalphabetic substitution cipher and E(2) is a transposition

cipher (not involving the key). The product E(1)

k E(2) is a round. While here the

transposition cipher is very simple and is not determined by the key, this need not be the

case. _

1.36 Remark (confusion and diffusion) A substitution in a round is said to add confusion to the

encryption process whereas a transposition is said to add diffusion. Confusion is intended

to make the relationship between the key and ciphertext as complex as possible. Diffusion

refers to rearranging or spreading out the bits in the message so that any redundancy in the

plaintext is spread out over the ciphertext. A round then can be said to add both confusion

and diffusion to the encryption. Most modern block cipher systems apply a number of

rounds in succession to encrypt plaintext.

1.5.4 Stream ciphers

Stream ciphers form an important class of symmetric-key encryption schemes. They are, in

one sense, very simple block ciphers having block length equal to one. What makes them

useful is the fact that the encryption transformation can change for each symbol of plaintext

being encrypted. In situations where transmission errors are highly probable, stream

ciphers are advantageous because they have no error propagation. They can also be used

when the datamust be processed one symbol at a time (e.g., if the equipment has no memory

or buffering of data is limited).

1.37 Definition Let K be the key space for a set of encryption transformations. A sequence of

symbols e1e2e3 _ _ _ ei 2 K, is called a keystream.

1.38 Definition Let A be an alphabet of q symbols and let Ee be a simple substitution cipher

with block length 1 where e 2 K. Letm1m2m3 _ _ _ be a plaintext string and let e1e2e3 _ _ _

be a keystream fromK. Astream cipher takes the plaintext string and produces a ciphertext

string c1c2c3 _ _ _ where ci = Eei (mi). If di denotes the inverse of ei, then Ddi(ci) = mi

decrypts the ciphertext string.

A stream cipher applies simple encryption transformations according to the keystream

being used. The keystream could be generated at random, or by an algorithm which generates

the keystream from an initial small keystream (called a seed), or from a seed and

previous ciphertext symbols. Such an algorithm is called a keystream generator.

The Vernam cipher

A motivating factor for the Vernam cipher was its simplicity and ease of implementation.

1.39 Definition The Vernam Cipher is a stream cipher defined on the alphabet A = f0; 1g. A

binary message m1m2 _ _ _mt is operated on by a binary key string k1k2 _ _ _ kt of the same

length to produce a ciphertext string c1c2 _ _ _ ct where

ci = mi _ ki; 1 _ i _ t:

If the key string is randomly chosen and never used again, the Vernam cipher is called a

one-time system or a one-time pad.

To see how the Vernam cipher corresponds to Definition 1.38, observe that there are

precisely two substitution ciphers on the set A. One is simply the identity map E0 which

sends 0 to 0 and 1 to 1; the other E1 sends 0 to 1 and 1 to 0. When the keystream contains

a 0, apply E0 to the corresponding plaintext symbol; otherwise, apply E1.

If the key string is reused there are ways to attack the system. For example, if c1c2 _ _ _ ct

and c0

1c0

2 _ _ _ c0

t are two ciphertext strings produced by the same keystream k1k2 _ _ _ kt then

ci = mi _ ki; c0

i = m0

i _ ki

and ci _ c0

i = mi _m0

i. The redundancy in the latter may permit cryptanalysis.

The one-time pad can be shown to be theoretically unbreakable. That is, if a cryptanalyst

has a ciphertext string c1c2 _ _ _ ct encrypted using a random key string which has been

used only once, the cryptanalyst can do no better than guess at the plaintext being any binary

string of length t (i.e., t-bit binary strings are equally likely as plaintext). It has been

proven that to realize an unbreakable system requires a random key of the same length as the

message. This reduces the practicality of the system in all but a few specialized situations.

Reportedly until very recently the communication line between Moscow and Washington

was secured by a one-time pad. Transport of the key was done by trusted courier.